
| A. | $f({-\frac{3}{2}})>f({{a^2}+2a+\frac{5}{2}})$ | B. | $f({-\frac{3}{2}})<f({{a^2}+2a+\frac{5}{2}})$ | C. | $f({-\frac{3}{2}})≥f({{a^2}+2a+\frac{5}{2}})$ | D. | $f({-\frac{3}{2}})≤f({{a^2}+2a+\frac{5}{2}})$ |
分析 根據題意,分析函數f(x)在區間[0,+∞)的單調性,由函數為偶函數可得$f({-\frac{3}{2}})$=f($\frac{3}{2}$),分析可得a2+2a+$\frac{5}{2}$=(a+1)2+$\frac{3}{2}$≥$\frac{3}{2}$,結合函數在[0,+∞)的單調性分析可得答案.
解答 解:根據題意,在[0,+∞)上函數$f(x)=\left\{\begin{array}{l}{({\frac{3}{4}})^x},x<1\\ 3-\frac{9}{4}x,x≥1\end{array}\right.$,
則函數在區間(1,+∞)上為減函數,
若f(x)是偶函數,則$f({-\frac{3}{2}})$=f($\frac{3}{2}$),
又由a2+2a+$\frac{5}{2}$=(a+1)2+$\frac{3}{2}$≥$\frac{3}{2}$,
則有f($\frac{3}{2}$)≥f(a2+2a+$\frac{5}{2}$),
即f(-$\frac{3}{2}$)≥f(a2+2a+$\frac{5}{2}$),
故選:C.
點評 本題考查函數奇偶性與單調性的綜合應用,關鍵是分析函數在區間[0,+∞)上的單調性.


 手拉手全優練考卷系列答案
手拉手全優練考卷系列答案科目:高中數學 來源: 題型:解答題
查看答案和解析>>
科目:高中數學 來源: 題型:解答題
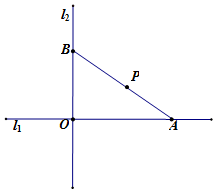 如圖所示,互相垂直的兩條道路l1、l2相交于O點,點P與l1、l2的距離分別為2千米、3千米,過點P建一條直線道路AB,與l1、l2分別交于A、B兩點.
如圖所示,互相垂直的兩條道路l1、l2相交于O點,點P與l1、l2的距離分別為2千米、3千米,過點P建一條直線道路AB,與l1、l2分別交于A、B兩點. 查看答案和解析>>
科目:高中數學 來源: 題型:選擇題
| A. | $\frac{1}{2}$ | B. | $\frac{\sqrt{2}}{2}$ | C. | 1 | D. | $\sqrt{2}$ |
查看答案和解析>>
科目:高中數學 來源: 題型:填空題
查看答案和解析>>
科目:高中數學 來源: 題型:解答題
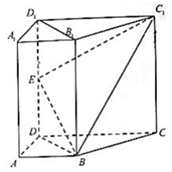 如圖,直四棱柱ABCD-A1B1C1D1中,AB∥CD,AB⊥AD,AD=AB=1.AA1=CD=2.E為棱DD1的中點.
如圖,直四棱柱ABCD-A1B1C1D1中,AB∥CD,AB⊥AD,AD=AB=1.AA1=CD=2.E為棱DD1的中點.查看答案和解析>>
科目:高中數學 來源: 題型:填空題
查看答案和解析>>
科目:高中數學 來源: 題型:選擇題
| A. | x-3y=0 | B. | x+3y=0 | C. | 3x-y=0 | D. | 3x+y=0 |
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com