
分析 (1)左焦點F(-2$\sqrt{2}$,0),直線AB方程為y=$\frac{\sqrt{3}}{3}$(x+2$\sqrt{2}$),設A(x1,y1),B(x2,y2).與橢圓方程聯立化為4x2+12$\sqrt{2}$x+15=0,再利用弦長公式即可得出,
(2)設AB中點M的坐標為(x0,y0),由(1)可知,x0=$\frac{1}{2}$(x1+x2)=-$\frac{3\sqrt{2}}{2}$,y0=$\frac{\sqrt{6}}{6}$,再根據兩點之間的距離公式即可求出.
解答 解:(1)左焦點F(-2$\sqrt{2}$,0),
直線AB方程為:y=$\frac{\sqrt{3}}{3}$(x+2$\sqrt{2}$)
設A(x1,y1),B(x2,y2).
聯立$\left\{\begin{array}{l}{y=\frac{\sqrt{3}}{3}(x+2\sqrt{2})}\\{\frac{{x}^{2}}{9}+{y}^{2}=1}\end{array}\right.$,化為4x2+12$\sqrt{2}$x+15=0,
∴x1+x2=-3$\sqrt{2}$,x1x2=$\frac{15}{4}$,
∴|x1-x2|2=(x1+x2)2-4x1x2=18-15=3,
∴|x1-x2|=$\sqrt{3}$
∴|AB|=$\sqrt{1+{k}^{2}}$•|x1-x2|=$\sqrt{\frac{4}{3}×3}$=2;
(2)設AB中點M的坐標為(x0,y0)
由(1)可知,x0=$\frac{1}{2}$(x1+x2)=-$\frac{3\sqrt{2}}{2}$,
y0=$\frac{\sqrt{3}}{3}$(x0+2$\sqrt{2}$)=$\frac{\sqrt{6}}{6}$,
∴|F1M|=$\sqrt{(-2\sqrt{2}+\frac{3\sqrt{2}}{2})^{2}+(\frac{\sqrt{6}}{6})^{2}}$=$\frac{\sqrt{6}}{3}$.
點評 本題考查了橢圓的標準方程、直線與橢圓相交弦長問題,兩點之間的距離公式,推理能力與計算能力,屬于中檔題.


科目:高中數學 來源: 題型:選擇題
| A. | $3+2\sqrt{2}$ | B. | $4\sqrt{2}$ | C. | 4+2$\sqrt{3}$ | D. | $4\sqrt{3}$ |
查看答案和解析>>
科目:高中數學 來源: 題型:解答題
查看答案和解析>>
科目:高中數學 來源: 題型:解答題
查看答案和解析>>
科目:高中數學 來源: 題型:選擇題
| A. | 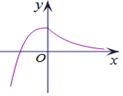 | B. | 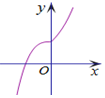 | C. | 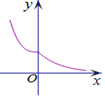 | D. | 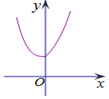 |
查看答案和解析>>
科目:高中數學 來源: 題型:選擇題
| A. | 在區間(-∞,3]上遞增 | B. | 在區間(-∞,-1]上遞增 | ||
| C. | 在區間(-∞,3]上遞減 | D. | 在區間(-∞,-1]上遞減 |
查看答案和解析>>
科目:高中數學 來源: 題型:解答題
 已知函數f(x)=$\left\{\begin{array}{l}ax+b,x<0\\{2^x},x≥0\end{array}\right.$,且f(-2)=3,f(-1)=f(1).
已知函數f(x)=$\left\{\begin{array}{l}ax+b,x<0\\{2^x},x≥0\end{array}\right.$,且f(-2)=3,f(-1)=f(1).查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com