
| A. | $3+2\sqrt{2}$ | B. | $4\sqrt{2}$ | C. | 4+2$\sqrt{3}$ | D. | $4\sqrt{3}$ |
分析 根據對數函數的性質先求出A的坐標,代入直線方程可得m、n的關系,再利用1的代換結合均值不等式求解即可.
解答 解:∵x=-2時,y=loga1-1=-1,
∴函數y=loga(x+3)-1(a>0,a≠1)的圖象恒過定點(-2,-1)即A(-2,-1),
∵點A在直線mx+ny+1=0上,
∴-2m-n+1=0,即2m+n=1,
∵mn>0,
∴m>0,n>0,$\frac{1}{m}+\frac{1}{n}$=($\frac{1}{m}+\frac{1}{n}$)(2m+n)=2+1+$\frac{n}{m}$+$\frac{2m}{n}$≥3+2•$\sqrt{\frac{n}{m}•\frac{2m}{n}}$=$3+2\sqrt{2}$,
當且僅當m=1-$\frac{\sqrt{2}}{2}$,n=$\sqrt{2}-$1時取等號.
故選:A
點評 本題考查了對數函數的性質和均值不等式等知識點,運用了整體代換思想,是高考考查的重點內容.


 閱讀快車系列答案
閱讀快車系列答案科目:高中數學 來源: 題型:選擇題
| A. | $-\frac{3}{5}$ | B. | $-\frac{6}{5}$ | C. | $\frac{6}{5}$ | D. | $\frac{3}{5}$ |
查看答案和解析>>
科目:高中數學 來源: 題型:解答題
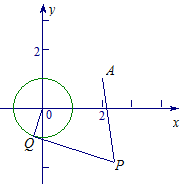 已知圓O:x2+y2=1和定點A(2,1),由圓O外一點P(a,b)向圓O引切線PQ,切點為Q,且滿足|PQ|=|PA|.
已知圓O:x2+y2=1和定點A(2,1),由圓O外一點P(a,b)向圓O引切線PQ,切點為Q,且滿足|PQ|=|PA|.查看答案和解析>>
科目:高中數學 來源: 題型:解答題
查看答案和解析>>
科目:高中數學 來源: 題型:解答題
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com