
分析 (1)由等差數列的求和公式和等比數列可得關于a1的方程,解方程可得a1.然后根據等差數列的通項公式進行解答;
(2)由已知:bn=$\frac{{a}_{n}}{{2}^{n}}$,由此利用錯位相減法能求出數列{bn}的前n項和Tn.
解答 解:(1)依題意得:S1+1=a1+1,S2=2a1+2,S3-1=3a1+6-1=3a1+5.
∵S1+1,S2,S3-1成等比數列,
∴(2a1+2)2=(a1+1)(3a1+5),
解得a1=1或a1=-1.
∵數列{an}是正項數列,
∴a1=1,
∴an=2n-1.
(2)由(1)知,an=2n-1.則bn=$\frac{{a}_{n}}{{2}^{n}}$=$\frac{2n-1}{{2}^{n}}$,
則數列{bn}的前n項和為Tn=$\frac{1}{2}$+$\frac{3}{{2}^{2}}$+$\frac{5}{{2}^{3}}$+…+$\frac{2n-3}{{2}^{n-1}}$+$\frac{2n-1}{{2}^{n}}$,①
所以$\frac{1}{2}$Tn=$\frac{1}{{2}^{2}}$+$\frac{3}{{2}^{3}}$+$\frac{5}{{2}^{4}}$+…+$\frac{2n-3}{{2}^{n}}$+$\frac{2n-1}{{2}^{n+1}}$,②
由①-②得:$\frac{1}{2}$Tn=$\frac{1}{2}$+2($\frac{1}{{2}^{2}}$+$\frac{1}{{2}^{3}}$+$\frac{1}{{2}^{4}}$+…+$\frac{1}{{2}^{n}}$)-$\frac{2n-1}{{2}^{n+1}}$=$\frac{1}{2}$+2×$\frac{\frac{1}{4}(1-\frac{1}{{2}^{n-1}})}{1-\frac{1}{2}}$-$\frac{2n-1}{{2}^{n+1}}$=$\frac{3}{2}$-$\frac{1}{{2}^{n-1}}$-$\frac{2n-1}{{2}^{n+1}}$.
故Tn=3-$\frac{1}{{2}^{2-n}}$-$\frac{2n-1}{{2}^{n}}$.
點評 本題考查數列的通項公式和前n項和的求法,是基礎題,解題時要認真審題,注意錯位相減法的合理運用.


 課前課后同步練習系列答案
課前課后同步練習系列答案 課堂小作業系列答案
課堂小作業系列答案 黃岡小狀元口算速算練習冊系列答案
黃岡小狀元口算速算練習冊系列答案 成功訓練計劃系列答案
成功訓練計劃系列答案 倍速訓練法直通中考考點系列答案
倍速訓練法直通中考考點系列答案科目:高中數學 來源: 題型:選擇題
| A. | a=18,B=30°,A=120° | B. | a=60,c=48,C=120° | ||
| C. | a=3,b=6,A=30° | D. | a=14,b=15,A=45° |
查看答案和解析>>
科目:高中數學 來源: 題型:解答題
查看答案和解析>>
科目:高中數學 來源: 題型:解答題
查看答案和解析>>
科目:高中數學 來源: 題型:選擇題
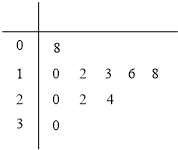 已知如圖是某NBA球員連續10場常規賽得分的莖葉圖,則該球員這10場比賽的場均得分為( )
已知如圖是某NBA球員連續10場常規賽得分的莖葉圖,則該球員這10場比賽的場均得分為( )| A. | 17.3 | B. | 17.5 | C. | 18.2 | D. | 18.4 |
查看答案和解析>>
科目:高中數學 來源: 題型:選擇題
| A. | [-1,4] | B. | [0,16] | C. | [-2,2] | D. | [1,4] |
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com