Question

5．設函數y=Asin（ωx+φ）（ω＞0，φ＞0）滿足：在一個周期內，當x=-$\frac{2}{5}$π時，函數有最大值2，當x=$\frac{8}{5}$π時，函數有最小值-2．
（1）求實數A，ω，φ的值；
（2）求該函數的單調增區間；
（3）用五點作圖法作出這個函數的大致圖象．

Answer 1

分析 （1）根據函數的最大值求得A=2，根據相鄰的最大值最小值之間的距離，求得T，利用周期公式可求ω，將（$\frac{8}{5}$π，-2），代入y=2sin（2x+φ），求得φ．
（2）令2kπ-$\frac{π}{2}$≤$\frac{1}{2}$x+$\frac{7π}{10}$≤2kπ+$\frac{π}{2}$，k∈Z，解得函數的單調增區間．
（3）求出對應的五點，利用“五點作圖法”畫出函數y=f（x）在一個周期上的圖象．

解答 解：（1）由函數的最小值為-2，
∴A=2，$\frac{T}{2}$=$\frac{8}{5}$π-（-$\frac{2}{5}$π）=2π，T=4π，
∴ω=$\frac{2π}{T}$=$\frac{1}{2}$，可得：y=2sin（$\frac{1}{2}$x+φ），
∵函數圖形過點（ $\frac{8}{5}$π，-2），代入y=2sin（$\frac{1}{2}$x+φ），可得：$\frac{4π}{5}$+φ=2kπ+$\frac{3π}{2}$，k∈Z，
∴φ=2kπ+$\frac{7π}{10}$，k∈Z，
∵φ＞0
∴當k=0時，可得φ=$\frac{7π}{10}$．
（2）由（1）可得：y=2sin（$\frac{1}{2}$x+$\frac{7π}{10}$），
令2kπ-$\frac{π}{2}$≤$\frac{1}{2}$x+$\frac{7π}{10}$≤2kπ+$\frac{π}{2}$，k∈Z，解得：4kπ-$\frac{12π}{5}$≤x≤4kπ-$\frac{2π}{5}$，k∈Z，
可得函數的單調增區間為：[4kπ-$\frac{12π}{5}$，4kπ-$\frac{2π}{5}$]，k∈Z，
（3）列表如下：

x	-$\frac{7π}{5}$	-$\frac{2π}{5}$	$\frac{3π}{5}$	$\frac{8π}{5}$	$\frac{13π}{5}$
$\frac{1}{2}$x+$\frac{7π}{10}$	0	$\frac{π}{2}$	π	$\frac{3π}{2}$	2π
y=2sin（$\frac{1}{2}$x+$\frac{7π}{10}$）	0	2	0	-2	0

描出五個關鍵點并光滑連線，得到一個周期的簡圖；圖象如下：

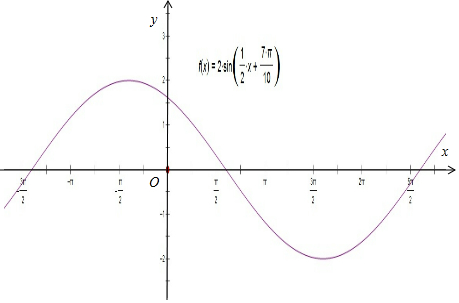
點評 本題考查求正弦函數解析式的方法，考查三角函數的圖象和性質，也考查了五點作圖法畫函數y=Asin（ωx+φ）的圖象的應用問題，是基礎題目．