

| A. | 在區間(-2,1)上f(x)是增函數 | B. | 在(1,3)上f(x)是減函數 | ||
| C. | 當x=4時,f(x)取極大值 | D. | 在(4,5)上f(x)是增函數 |
分析 由于f′(x)≥0⇒函數f(x)單調遞增;f′(x)≤0⇒單調f(x)單調遞減,觀察f′(x)的圖象可知,通過觀察f′(x)的符號判定函數的單調性即可.
解答 解:由于f′(x)≥0⇒函數f(x)單調遞增;f′(x)≤0⇒單調f(x)單調遞減
觀察f′(x)的圖象可知,
當x∈(-2,1)時,函數先遞減,后遞增,故A錯誤
當x∈(1,3)時,函數先增后減,故B錯誤
當x∈(4,5)時函數遞增,故D正確
由函數的圖象可知函數在x=4處取得函數的極小值,故C錯誤
故選:D.
點評 本題主要考查了導數的應用:通過導數的符號判定函數單調性,要注意不能直接看導函數的單調性,而是通過導函數的正負判定原函數的單調性.


科目:高中數學 來源: 題型:選擇題
| A. | k-1 | B. | k | C. | k+1 | D. | k2 |
查看答案和解析>>
科目:高中數學 來源: 題型:解答題
查看答案和解析>>
科目:高中數學 來源: 題型:解答題
查看答案和解析>>
科目:高中數學 來源: 題型:解答題
查看答案和解析>>
科目:高中數學 來源: 題型:選擇題
| A. | (-∞,-2012) | B. | (-2016,-2012) | C. | (-∞,-2016) | D. | (-2016,0) |
查看答案和解析>>
科目:高中數學 來源: 題型:解答題
查看答案和解析>>
科目:高中數學 來源: 題型:解答題
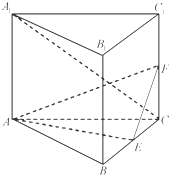 如圖,直三棱柱ABC-A1B1C1的底面是邊長為2的正三角形,AA1=$\sqrt{2}$,E,F分別是BC,CC1的中點.
如圖,直三棱柱ABC-A1B1C1的底面是邊長為2的正三角形,AA1=$\sqrt{2}$,E,F分別是BC,CC1的中點.查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com