
分析 (Ⅰ)當a=2時,$f(x)=ln(1+x)-\frac{2x}{1+x}$,f(1)=ln2-1,k=f′(1)=0,由此能求出切線方程.
(Ⅱ)${f^'}(x)=\frac{1}{1+x}-\frac{{a({x+1})-ax}}{{{{({1+x})}^2}}}=\frac{x+1-a}{{{{({1+x})}^2}}}=\frac{{x-({a-1})}}{{{{({x+1})}^2}}}$,由此利用導數性質和分類討論思想能求出當且僅當a=1時f(x)≥0恒成立.
解答 解:(Ⅰ)當a=2時,$f(x)=ln(1+x)-\frac{2x}{1+x}$,f(1)=ln2-1,…(1分),
${f^'}(x)=\frac{1}{1+x}-\frac{{2({x+1})-2x}}{{{{({1+x})}^2}}}=\frac{x-1}{{{{({1+x})}^2}}}$,…(2分)
∴k=f′(1)=0,…(3分)
∴切線方程為y=ln2-1.…(4分)
(Ⅱ)${f^'}(x)=\frac{1}{1+x}-\frac{{a({x+1})-ax}}{{{{({1+x})}^2}}}=\frac{x+1-a}{{{{({1+x})}^2}}}=\frac{{x-({a-1})}}{{{{({x+1})}^2}}}$.
①當a≤0時,a-1≤-1,又x∈(-1,+∞),
∴x-(a-1)>0,∴f′(x)>0,∴f(x)在(-1,+∞)上為增函數,…(6分)
又∵f(0)=0,∴當-1<x<0時,f(x)<0,與題意不符.…(7分)
②當a>0,令f′(x)=0,得x=a-1>-1,
且-1<x<a-1時,f′(x)<0,x>a-1時,f′(x)>0,
∴f(x)在x=a-1時有極小值,也是最小值,
∴f(x)min=f(a-1)=lna-a+1≥0,…(9分)
記g(x)=lnx-x+1,則${g^'}(x)=\frac{1}{x}-1=-\frac{x-1}{x}$,
令g′(x)=0,得x=1,
當0<x<1時,g′(x)>0,當x>1時,g′(x)<0,
∴g(x)在x=1處有極大值就是最大值為g(1)=0,…(11分)
∴lna-a+1最大值為0,
又lna-a+1≥0,故a=1,
即當且僅當a=1時f(x)≥0恒成立.…(12分)
點評 本題考查切線方程的求法,考查實數的取值范圍的求法,是中檔題,解題時要認真審題,注意導數性質的合理運用.


科目:高中數學 來源: 題型:選擇題

| A. | 在區間(-2,1)上f(x)是增函數 | B. | 在(1,3)上f(x)是減函數 | ||
| C. | 當x=4時,f(x)取極大值 | D. | 在(4,5)上f(x)是增函數 |
查看答案和解析>>
科目:高中數學 來源: 題型:填空題
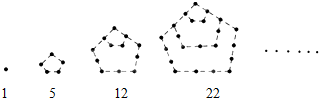 如圖中的實心點個數1,5,12,22,…,被稱為五角形數,其中第1個五角形數記作a1=1,第2個五角形數記作a2=5,第3個五角形數記作a3=12,第4個五角形數記作a4=22,…,若按此規律繼續下去,則an=$\frac{{3{n^2}-n}}{2}$.
如圖中的實心點個數1,5,12,22,…,被稱為五角形數,其中第1個五角形數記作a1=1,第2個五角形數記作a2=5,第3個五角形數記作a3=12,第4個五角形數記作a4=22,…,若按此規律繼續下去,則an=$\frac{{3{n^2}-n}}{2}$.查看答案和解析>>
科目:高中數學 來源: 題型:選擇題
| A. | 2$\sqrt{2}$-3 | B. | 2$\sqrt{2}$-1 | C. | 2$\sqrt{2}$+3 | D. | 2$\sqrt{2}$+1 |
查看答案和解析>>
科目:高中數學 來源: 題型:選擇題
| A. | $\frac{1}{8}$ | B. | $\frac{2}{13}$ | C. | $\frac{11}{3}$ | D. | $\frac{1}{14}$ |
查看答案和解析>>
科目:高中數學 來源: 題型:解答題
 如圖,在四棱錐P-ABCD中,底面ABCD為菱形,且AB=AC=2,O為AC的中點,PO⊥平面ABCD,M為PD的中點.
如圖,在四棱錐P-ABCD中,底面ABCD為菱形,且AB=AC=2,O為AC的中點,PO⊥平面ABCD,M為PD的中點.查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com