
 已知點$({\sqrt{2},2})$與點$({-2,-\frac{1}{2}})$分別在冪函數f(x),g(x)的圖象上.
已知點$({\sqrt{2},2})$與點$({-2,-\frac{1}{2}})$分別在冪函數f(x),g(x)的圖象上.分析 (1)由點$({\sqrt{2},2})$與點$({-2,-\frac{1}{2}})$分別在冪函數f(x),g(x)的圖象上,可得函數的解析式,進而畫出兩個函數的圖象;
(2)數形結合,可以得到①當x<0,或x>1時,f(x)>g(x);②當x=1時,f(x)=g(x);③當0<x<1時,f(x)<g(x).
解答 解:(1)設f(x)=xa,g(x)=xb,
由點$({\sqrt{2},2})$與點$({-2,-\frac{1}{2}})$分別在冪函數f(x),g(x)的圖象上可得:
${\sqrt{2}}^{a}=2$,(-2)b=$-\frac{1}{2}$,
解得:a=2,b=-1,
故f(x)=x2,g(x)=x-1,
故在同一直角坐標系中畫出兩個函數的圖象,如圖所示: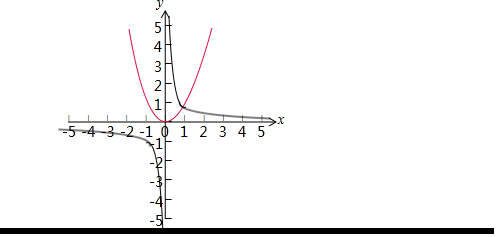
(2)由圖可得:
①當x<0,或x>1時,f(x)>g(x);
②當x=1時,f(x)=g(x);
③當0<x<1時,f(x)<g(x).
點評 本題考查的知識點是冪函數的圖象和性質,數形結合思想,難度不大,屬于基礎題.


 互動英語系列答案
互動英語系列答案 名牌學校分層周周測系列答案
名牌學校分層周周測系列答案 黃岡海淀全程培優測試卷系列答案
黃岡海淀全程培優測試卷系列答案科目:高中數學 來源: 題型:解答題
查看答案和解析>>
科目:高中數學 來源: 題型:選擇題
| A. | ($\frac{3}{2}$,2) | B. | (1,2] | C. | [$\frac{3}{2}$,2] | D. | (1,2) |
查看答案和解析>>
科目:高中數學 來源: 題型:解答題
查看答案和解析>>
科目:高中數學 來源: 題型:選擇題
| A. | M=N=P | B. | M?P=N | C. | M∩P=N | D. | N∩P=N |
查看答案和解析>>
科目:高中數學 來源: 題型:解答題
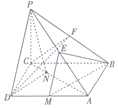 如圖,在四棱錐P-ABCD中,PC⊥底面ABCD,底面ABCD是矩形,BC=PC,E,F分別是PA,PB的中點.
如圖,在四棱錐P-ABCD中,PC⊥底面ABCD,底面ABCD是矩形,BC=PC,E,F分別是PA,PB的中點.查看答案和解析>>
科目:高中數學 來源: 題型:填空題
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com