Question

2．如圖，已知四棱錐P-ABCD中，底面ABCD為菱形，PA⊥平面ABCD，∠ABC=60°，E，F 分別是 BC，PC的中點．
（1）證明：AE⊥平面PAD
（2）取AB=2，若H為PD上的動點，EH與平面PAD所成最大角的正切值為$\frac{\sqrt{6}}{2}$時，求V_P-AEH的體積．

Answer 1

分析 （1）由四邊形ABCD為菱形，∠ABC=60°，推導出AE⊥BC，再由BC∥AD，得AE⊥AD，由PA⊥平面ABCD，得PA⊥AE，由此能證明AE⊥平面PAD．
（2）設AB=2，H為PD上任意一點，連結AH，EH，AE⊥平面PAD，則∠EHA為EH與平面PAD所成的角，當AH⊥PD時，∠EHA最大．此時tan∠EHA=$\frac{\sqrt{6}}{2}$，AH=$\sqrt{2}$，V_P-AEH的體積V_P-AEH=V_E-PAH，由此能求出結果．

解答 證明：（1）由四邊形ABCD為菱形，∠ABC=60°，可得△ABC為正三角形．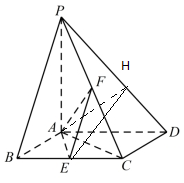
∵E為BC的中點，∴AE⊥BC．
又BC∥AD，因此AE⊥AD．
∵PA⊥平面ABCD，AE?平面ABCD，∴PA⊥AE．
而PA?平面PAD，AD?平面PAD且PA∩AD=A，
∴AE⊥平面PAD．
解：（2）設AB=2，H為PD上任意一點，連結AH，EH．
由（1）知AE⊥平面PAD，則∠EHA為EH與平面PAD所成的角．
在Rt△EAH中，AE=$\sqrt{3}$，
∴當AH最短時，∠EHA最大，
即當AH⊥PD時，∠EHA最大．此時tan∠EHA=$\frac{\sqrt{6}}{2}$，
因此AH=$\sqrt{2}$．
又AD=2，∴∠ADH=45°，∴PA=AD tan 45°=2．
∴V_P-AEH=V_E-PAH=$\frac{1}{3}{S}_{△PAH}•AE$
=$\frac{1}{3}（\frac{1}{2}×AH×PH）×AE$
=$\frac{1}{3}×（\frac{1}{2}×\sqrt{2}×\sqrt{2}）×\sqrt{3}$
=$\frac{\sqrt{3}}{3}$．

點評 本題考查線面垂直的證明，考查三棱錐的體積的求法，考查空間中線線、線面、面面間的位置關系等基礎知識，考查推理論證能力、運算求解能力，考查化歸與轉化思想、函數與方程思想，是中檔題．