
分析 (1)先求出導函數,再根據導數和函數的單調性關系求出單調區,即可得到函數的極值,
(2)分離參數,構造函數,根據導數和函數的最值得關系即可求出參數k的取值范圍.
解答 解:(1)函數f(x)的定義域為(0,+∞),
∴f′(x)=$\frac{m-lnx}{{x}^{2}}$,
令f′(x)=0,解得x=em,
當x∈(0,em)時,f′(x)>0,f(x)單調遞增,
當x∈(em,+∞)時,f′(x)<0,f(x)單調遞減,
當x=em時,f(x)有極大值,且極大值為f(em)=e-m,
(2)f(x)≥$\frac{k}{x+1}$對x∈[1,+∞)恒成立,
∴k≤$\frac{x+11+lnx}{x}$對x∈[1,+∞)恒成立,
令g(x)=$\frac{x+11+lnx}{x}$,
∴g′(x)=$\frac{x-lnx}{{x}^{2}}$,
令h(x)=x-lnx,
則h′(x)=1-$\frac{1}{x}$,
∵x>1,
∴h′(x)≥0,
∴h(x)在[1,+∞)上單調遞增,
∴h(x)≥h(1)=1>0,
∴g′(x)>0,
∴g(x)在[1,+∞)上單調遞增,
∴g(x)min=g(1)=2,
∴k≤2,
故k的取值范圍為(-∞,2]
點評 本題考查了導數和函數的極值和最值得關系,以及參數的取值范圍和恒成立的問題,屬于中檔題.


科目:高中數學 來源: 題型:選擇題
| A. | -2 | B. | 2 | C. | -2或2 | D. | 0 |
查看答案和解析>>
科目:高中數學 來源: 題型:解答題
 在如圖所示的幾何體中,四邊形ABCD是等腰梯形,AB∥CD,AB=2CB=2,∠ABC=60°,在梯形ACEF中,EF∥AC,且AC=2EF=2EC,EC⊥平面ABCD.
在如圖所示的幾何體中,四邊形ABCD是等腰梯形,AB∥CD,AB=2CB=2,∠ABC=60°,在梯形ACEF中,EF∥AC,且AC=2EF=2EC,EC⊥平面ABCD.查看答案和解析>>
科目:高中數學 來源: 題型:解答題
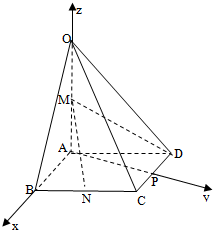 如圖,在四棱錐O-ABCD中,底面ABCD是菱形,∠ABC=60°,OA=AB=2,OA⊥底面ABCD,M為OA的中點,N為BC的中點.作AP⊥CD于點P,分別以AB,AP,AO所在直線為x,y,z軸,建立如圖空間直角坐標系.
如圖,在四棱錐O-ABCD中,底面ABCD是菱形,∠ABC=60°,OA=AB=2,OA⊥底面ABCD,M為OA的中點,N為BC的中點.作AP⊥CD于點P,分別以AB,AP,AO所在直線為x,y,z軸,建立如圖空間直角坐標系.查看答案和解析>>
科目:高中數學 來源: 題型:填空題
查看答案和解析>>
科目:高中數學 來源: 題型:解答題
查看答案和解析>>
科目:高中數學 來源: 題型:解答題
查看答案和解析>>
科目:高中數學 來源: 題型:解答題
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com