
分析 求出點(a,b)所在平面區域表示以(2,0)為圓心,1,3為半徑的圓環,即可得出結論.
解答 解:由題意,曲線$\left\{{\begin{array}{l}{x=cosϕ+a}\\{y=sinϕ+b}\end{array}}$(φ為參數),
表示以(a,b)為圓心,1為半徑的圓;曲線ρ=4cosθ,
即x2+y2=4x,表示以(2,0)為圓心,2為半徑的圓,
∵曲線$\left\{{\begin{array}{l}{x=cosϕ+a}\\{y=sinϕ+b}\end{array}}$(φ為參數)與曲線ρ=4cosθ相交,
∴1<(a-2)2+b2<9,表示以(2,0)為圓心,1,3為半徑的圓環.
(2,0)到直線x+$\sqrt{3}$y=0的距離為d=$\frac{2}{\sqrt{1+3}}$=1,
∴直線x+$\sqrt{3}$y=0被點(a,b)所在平面區域截得的弦長為2($\sqrt{9-1}$-0)=4$\sqrt{2}$.
故答案為4$\sqrt{2}$.
點評 本題考查參數方程、極坐標方程的轉化,考查軌跡方程,考查點到直線的距離公式,屬于中檔題.


科目:高中數學 來源: 題型:解答題
查看答案和解析>>
科目:高中數學 來源: 題型:解答題
查看答案和解析>>
科目:高中數學 來源: 題型:填空題
查看答案和解析>>
科目:高中數學 來源: 題型:解答題
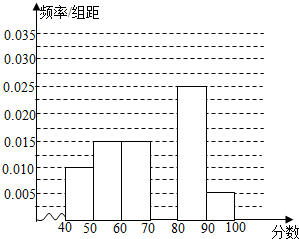 某校參加高一年級期中考試的學生中隨機抽取60名學生,將其數學成績(均為整數)分成六段[40,50),[50,60),…,[90,100)后得到如下部分頻率分布直方圖.觀察圖形的信息,回答下列問題:
某校參加高一年級期中考試的學生中隨機抽取60名學生,將其數學成績(均為整數)分成六段[40,50),[50,60),…,[90,100)后得到如下部分頻率分布直方圖.觀察圖形的信息,回答下列問題:查看答案和解析>>
科目:高中數學 來源: 題型:解答題
查看答案和解析>>
科目:高中數學 來源: 題型:解答題
查看答案和解析>>
科目:高中數學 來源: 題型:解答題
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com