
| A. | $18+6\sqrt{3}$ | B. | $18+8\sqrt{3}$ | C. | $18+9\sqrt{3}$ | D. | $18+10\sqrt{3}$ |
分析 判斷幾何體的體積最大時的位置,然后求解三棱錐的表面積.
解答 解:三棱錐A-BCD四個頂點都在半徑為3的球面上,且BC過球心,三棱錐A-BCD的體積最大,
可知BC是球的直徑,D在大圓上,當三角形DBC是等腰直角三角形時,面積最大,如果A與球心的連線與BCD平面垂直,則幾何體的體積最大;如圖:
則三棱錐A-BCD的表面積: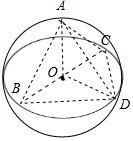
此時OA=OB=OD=OC=3,AB=AD=AC=3$\sqrt{2}$,
BD=DC=3$\sqrt{2}$,三棱錐的表面積為:2×$\frac{1}{2}×6×3$+2×$\frac{\sqrt{3}}{4}×(3\sqrt{2})^{2}$=18+9$\sqrt{3}$.
故選:C.
點評 本題考查幾何體的外接球,幾何體的體積與幾何體的位置關系的判斷,表面積的求法,考查空間想象能力以及計算能力.


科目:高中數學 來源: 題型:解答題
查看答案和解析>>
科目:高中數學 來源: 題型:選擇題
| A. | $\frac{5π}{8}$ | B. | $\frac{11π}{16}$ | C. | $\frac{9π}{16}$ | D. | $\frac{7π}{8}$ |
查看答案和解析>>
科目:高中數學 來源: 題型:填空題
查看答案和解析>>
科目:高中數學 來源: 題型:選擇題
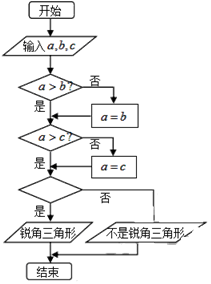 如圖程序框圖中,若輸入互不相等的三個正實數a,b,c,要求判斷△ABC的形狀,則空白的判斷框中應填入( )
如圖程序框圖中,若輸入互不相等的三個正實數a,b,c,要求判斷△ABC的形狀,則空白的判斷框中應填入( )| A. | a2+b2>c2? | B. | a2+c2>b2? | C. | b2+c2>a2? | D. | b2+a2=c2? |
查看答案和解析>>
科目:高中數學 來源: 題型:選擇題
| A. | $\frac{1}{16}$ | B. | $\frac{1}{8}$ | C. | $\frac{1}{4}$ | D. | $\frac{1}{2}$ |
查看答案和解析>>
科目:高中數學 來源: 題型:選擇題
| A. | $\frac{π}{6}$ | B. | $\frac{π}{4}$ | C. | $\frac{π}{3}$ | D. | $\frac{π}{2}$ |
查看答案和解析>>
科目:高中數學 來源: 題型:填空題
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com