
分析 (1)sin(A-B)=$\frac{a}{a+b}$sinAcosB-$\frac{b}{a+b}$sinBcosA,展開利用正弦定理可得:acosB-bcosA=$\frac{{a}^{2}}{a+b}$cosB-$\frac{{b}^{2}}{a+b}$cosA,化簡即可證明.
(2)A=B,可得b=a=$\sqrt{6}$.c=2bcosA,可得S△ABC=$\frac{1}{2}$bcsinA=3sin$\frac{7π}{12}$=3sin$(\frac{π}{4}+\frac{π}{3})$,展開即可得出.
解答 (1)證明:∵sin(A-B)=$\frac{a}{a+b}$sinAcosB-$\frac{b}{a+b}$sinBcosA,
∴sinAcosB-cosAsinB=$\frac{a}{a+b}$sinAcosB-$\frac{b}{a+b}$sinBcosA,
利用正弦定理可得:acosB-bcosA=$\frac{{a}^{2}}{a+b}$cosB-$\frac{{b}^{2}}{a+b}$cosA,
化為:cosA=cosB,又A,B∈(0,π),
∴A=B.
(2)解:∵A=B,∴b=a=$\sqrt{6}$.
∴c=2bcosA=2$\sqrt{6}$cos$\frac{7π}{24}$,
∴S△ABC=$\frac{1}{2}$bcsinA=$\frac{1}{2}×\sqrt{6}$×2$\sqrt{6}$cos$\frac{7π}{24}$×sin$\frac{7π}{24}$
=3sin$\frac{7π}{12}$=3sin$(\frac{π}{4}+\frac{π}{3})$=3$(\frac{\sqrt{2}}{2}×\frac{1}{2}+\frac{\sqrt{2}}{2}×\frac{\sqrt{3}}{2})$=$\frac{3(\sqrt{2}+\sqrt{6})}{4}$.
點評 本題考查了正弦定理、倍角公式、三角形面積計算公式,考查了推理能力與計算能力,屬于中檔題.


科目:高中數(shù)學(xué) 來源: 題型:選擇題
| A. | ex2-ex1>lnx2-lnx1 | B. | ex2-ex1<lnx2-lnx1 | ||
| C. | x2ex1>x1ex2 | D. | x2ex1<x1ex2 |
查看答案和解析>>
科目:高中數(shù)學(xué) 來源: 題型:選擇題
| A. | -5 | B. | -4 | C. | -2$\sqrt{5}$ | D. | -3 |
查看答案和解析>>
科目:高中數(shù)學(xué) 來源: 題型:選擇題
| A. | 充分不必要條件 | B. | 必要不充分條件 | ||
| C. | 充分必要條件 | D. | 既不充分也不必要條件 |
查看答案和解析>>
科目:高中數(shù)學(xué) 來源: 題型:選擇題
| A. | 1 | B. | 2 | C. | $\frac{5}{2}$ | D. | $\frac{3}{2}$ |
查看答案和解析>>
科目:高中數(shù)學(xué) 來源: 題型:選擇題
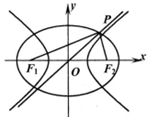 如圖,點F1、F2是橢圓C1、C2的左右焦點,橢圓C1與雙曲線C2的漸近線交于點P,PF1⊥PF2,橢圓C1與雙曲線C2的離心率分別為e1、e2,則( )
如圖,點F1、F2是橢圓C1、C2的左右焦點,橢圓C1與雙曲線C2的漸近線交于點P,PF1⊥PF2,橢圓C1與雙曲線C2的離心率分別為e1、e2,則( )| A. | e22=$\frac{1+{{e}_{1}}^{4}}{1-{{e}_{1}}^{2}}$ | B. | e22=$\frac{{2{e}_{1}}^{4}}{1-{{e}_{1}}^{2}}$ | ||
| C. | e22=$\frac{1-{{e}_{1}}^{4}}{2{{e}_{1}}^{2}-1}$ | D. | e22=$\frac{{{e}_{1}}^{4}}{2{{e}_{1}}^{2}-1}$ |
查看答案和解析>>
科目:高中數(shù)學(xué) 來源: 題型:填空題
查看答案和解析>>
科目:高中數(shù)學(xué) 來源: 題型:選擇題
| A. | $\frac{x^2}{16}+\frac{y^2}{9}=1$ | B. | $\frac{x^2}{5}+\frac{y^2}{4}=1$ | C. | $\frac{x^2}{9}+\frac{y^2}{5}=1$ | D. | $\frac{x^2}{25}+\frac{y^2}{20}=1$ |
查看答案和解析>>
科目:高中數(shù)學(xué) 來源: 題型:填空題
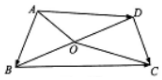 如圖,在平面四邊形ABCD中,O為BD的中點,且OA=3,OC=5,若$\overrightarrow{AB}$•$\overline{AD}$=-7,則$\overrightarrow{BC}$•$\overrightarrow{DC}$的值是9.
如圖,在平面四邊形ABCD中,O為BD的中點,且OA=3,OC=5,若$\overrightarrow{AB}$•$\overline{AD}$=-7,則$\overrightarrow{BC}$•$\overrightarrow{DC}$的值是9.查看答案和解析>>
湖北省互聯(lián)網(wǎng)違法和不良信息舉報平臺 | 網(wǎng)上有害信息舉報專區(qū) | 電信詐騙舉報專區(qū) | 涉歷史虛無主義有害信息舉報專區(qū) | 涉企侵權(quán)舉報專區(qū)
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com