
分析 根據題意,由于數列{an}具有性質P以及a2=a5=2,分析可得a3=a6=3,a4=a7,a5=a8=3,結合題意可以將a6+a7+a8=21變形為a3+a4+a5=21,計算可得a4的值,進而分析可得a3=a6=a9=…a3n=3,a4=a7=a6=…a3n+1=15,a5=a8=…a3n+2=3,(n≥1);分析可得a2017的值.
解答 解:根據題意,數列{an}具有性質P,且a2=a5=2,
則有a3=a6=3,a4=a7,a5=a8=3,
若a6+a7+a8=21,可得a3+a4+a5=21,則a4=21-3-3=15,
進而分析可得:a3=a6=a9=…a3n=3,a4=a7=a6=…a3n+1=15,a5=a8=…a3n+2=3,(n≥1)
則a2017=a3×672+1=15,
故答案為:15.
點評 本題考查數列的表示方法,關鍵分析什么樣的數列具有性質P,并且求出a4的值,


 開心試卷期末沖刺100分系列答案
開心試卷期末沖刺100分系列答案 雙基同步導航訓練系列答案
雙基同步導航訓練系列答案 黃岡小狀元同步計算天天練系列答案
黃岡小狀元同步計算天天練系列答案科目:高中數學 來源: 題型:選擇題
| A. | ①② | B. | ②③ | C. | ③④ | D. | ①②③ |
查看答案和解析>>
科目:高中數學 來源: 題型:解答題
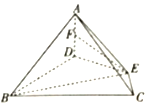 如圖,在四棱錐A-BCED中,AD⊥底面BCED,BD⊥DE,∠DBC=∠BCE═60°,BD=2CE.
如圖,在四棱錐A-BCED中,AD⊥底面BCED,BD⊥DE,∠DBC=∠BCE═60°,BD=2CE.查看答案和解析>>
科目:高中數學 來源: 題型:解答題
查看答案和解析>>
科目:高中數學 來源: 題型:選擇題
| A. | -$\frac{4}{5}$ | B. | $\frac{4}{5}$ | C. | -$\frac{4}{5}$i | D. | $\frac{4}{5}$i |
查看答案和解析>>
科目:高中數學 來源: 題型:選擇題
| A. | 40 | B. | 20 | C. | 31 | D. | 43 |
查看答案和解析>>
科目:高中數學 來源: 題型:選擇題
| A. | [-1,8) | B. | (0,5] | C. | [-1,5) | D. | (0,8) |
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com