
分析 (1)將a的值代入f(x),通過討論x的范圍,求出各個區間上的不等式否定解集,取并集即可;
(2)根據絕對值的性質,問題轉化為$|{x-\frac{a}{2}}|+|{x+\frac{a}{2}}|≥2$恒成立,求出a的范圍即可.
解答 解:(1)當a=2時,|2x-2|-|x|>1.
當x<0時,-2x+2+x>1,∴x<1,∴x<0
當0≤x<1時,-2x+2-x>1,∴$0≤x<\frac{1}{3}$;
當x≥1時,2x-2-x>1,∴x>3
故所求不等式的解集為$({-∞,\frac{1}{3}})∪({3,+∞})$…(5分)
(2)由f(x)≥4-|2x+a|-|x|得|2x-a|+|2x+a|≥4恒成立,
即$|{x-\frac{a}{2}}|+|{x+\frac{a}{2}}|≥2$恒成立,∴|a|≥2,
故實數的取值范圍為(-∞,-2]∪[2,+∞)…..(10分)
點評 本題考查了解絕對值不等式問題,考查分類討論思想以及轉化思想,是一道中檔題.


 小天才課時作業系列答案
小天才課時作業系列答案 一課四練系列答案
一課四練系列答案 黃岡小狀元滿分沖刺微測驗系列答案
黃岡小狀元滿分沖刺微測驗系列答案 新輔教導學系列答案
新輔教導學系列答案 陽光同學一線名師全優好卷系列答案
陽光同學一線名師全優好卷系列答案科目:高中數學 來源: 題型:解答題
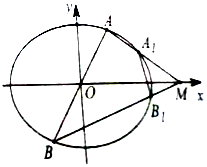 已知橢圓C:$\frac{x^2}{a^2}+\frac{y^2}{b^2}=1({a>b>0})$的離心率為$\frac{{\sqrt{2}}}{2}$,焦距為2,直線y=kx(x≠0)與橢圓C交于A,B兩點,M為其右準線與x軸的交點,直線AM,BM分別與橢圓C交于A1,B1兩點,記直線A1B1的斜率為k1
已知橢圓C:$\frac{x^2}{a^2}+\frac{y^2}{b^2}=1({a>b>0})$的離心率為$\frac{{\sqrt{2}}}{2}$,焦距為2,直線y=kx(x≠0)與橢圓C交于A,B兩點,M為其右準線與x軸的交點,直線AM,BM分別與橢圓C交于A1,B1兩點,記直線A1B1的斜率為k1查看答案和解析>>
科目:高中數學 來源: 題型:填空題
查看答案和解析>>
科目:高中數學 來源: 題型:選擇題
| A. | x2+y2=16 | B. | x2+y2=16(x≥4) | C. | x2-y2=16 | D. | x2-y2=16(x≥4) |
查看答案和解析>>
科目:高中數學 來源: 題型:解答題
查看答案和解析>>
科目:高中數學 來源: 題型:解答題
查看答案和解析>>
科目:高中數學 來源: 題型:選擇題
| A. | n | B. | n-1 | C. | $\frac{n(n-1)}{2}$ | D. | $\frac{1}{2}$n(n+1) |
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com