
分析 (1)求出導函數,根據切線的和導函數的關系求解 即可;、
(2)求出導函數f'(x)=(2x-2a)lnx,對a進行分類討論,在不同區間求出函數的單調性,進而判斷函數的最值問題;
(3)根據(2)可知a的范圍,得出f(x1)+f(x2)=f(a)+f(1),作差放縮可得$f({x_1})+f({x_2})-(\frac{1}{2}{a^2}+3a)$=$-{a^2}lna+{a^2}-a-\frac{1}{2}<-{a^2}(lna-1+\frac{1}{a})$,構造函數$g(a)=lna-1+\frac{1}{a}$,利用導函數得出函數的單調性,得出g(a)>g(1)=0,得出結論.
解答 解:(1)當a=0時,$f(x)={x^2}lnx-\frac{1}{2}{x^2}$,f'(x)=2xlnx,所以切線I的斜率k=f'(t)=2tlnt,又直線I過原點,所以k=tlnt-$\frac{1}{2}$t,
,由2tlnt=tlnt-$\frac{1}{2}$t,得lnt=-$\frac{1}{2}$,t=$\frac{1}{\sqrt{e}}$.所以k=f'(-$\frac{1}{\sqrt{e}}$)=-$\frac{1}{\sqrt{e}}$,故切線I的方程為y=-$\frac{x}{\sqrt{e}}$.
(2)由f(x)=(x2-2ax)lnx+2ax-$\frac{1}{2}$x2,可得f'(x)=(2x-2a)lnx,
①當a≤0時f'(x)>0得x>1,f'(x)<0得0<x<1,
f(x)在(1,+∞)上單調遞增,在(0,1)上單調遞減,f(x)在x=1時取到極小值,且f(1)=2a-$\frac{1}{2}$,f(x)沒有極大值.
②當0<a<1時,f'(x)>0得x>1或0<x<a,f'(x)<0得a<x<1.f(x)在(0,a),(1,+∞)上單調遞增,在(a,1)上單調遞減,
f(x)在x=a時取到極大值,且f(a)=-a2lna+$\frac{3}{2}{a}^{2}$,f(x)在x=1時取到極小值,且f(1)=2a-$\frac{1}{2}$;
③當a=1時f'(x)≥0恒成立恒成立,f(x)在R上單調遞增,f(x)沒有極大值也沒有極小值;
④當a>1時f'(x)>0得x>a或0<x<1,f'(x)<0得1<x<a,f(x)在(0,1),(a,+∞)上單調遞增,在(1,a)上單調遞減,f(x)在x=a時取到極小值,且f(a)=-a2lna+$\frac{3}{2}{a}^{2}$,.f(x)在x=1時取到極大值,且f(1)=2a-$\frac{1}{2}$;
綜上可得,當a≤0時,f(x)在x=1時取到極小值2a-$\frac{1}{2}$,f(x)沒有極大值;
當0<a<1時,f(x)在x=a時取到極大值-a2lna+$\frac{3}{2}{a}^{2}$,在x=1時取到極小值2a-$\frac{1}{2}$;
當a=1時,f(x)沒有極大值也沒有極小值;
當a>1時,f(x)在x=a時取到極小值$-{a^2}lna+\frac{3}{2}{a^2}$,在x=1時取到極大值$2a-\frac{1}{2}$.
(3)由(2)知當a>0且a≠1時,f(x)有兩個極值f(x)點x1,x2,且f(x1)+f(x2)=f(a)+f(1),$f({x_1})+f({x_2})-(\frac{1}{2}{a^2}+3a)$=$-{a^2}lna+{a^2}-a-\frac{1}{2}<-{a^2}(lna-1+\frac{1}{a})$,
設$g(a)=lna-1+\frac{1}{a}$,則$g'(a)=\frac{1}{a}-\frac{1}{a^2}=\frac{a-1}{a^2}$,所以g(a)在(0,1)上單調遞減,在(1,+∞)上單調遞增,由a>0且a≠1可得g(a)>g(1)=0,所以$f({x_1})+f({x_2})-(\frac{1}{2}{a^2}+3a)<$$-{a^2}(lna-1+\frac{1}{a})<0$,即$f({x_1})+f({x_2})<\frac{1}{2}{a^2}+3a$.
點評 本題考查了導函數的綜合應用和參數的分類討論,難點是參數的討論和函數的構造.


 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小學生10分鐘應用題系列答案
小學生10分鐘應用題系列答案科目:高中數學 來源: 題型:填空題
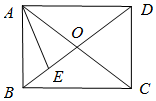 在矩形ABCD中,對角線AC,BD相交于點O,E為BO的中點,若$\overrightarrow{AE}=λ\overrightarrow{AB}+μ\overrightarrow{AD}$(λ,μ為實數),則λμ=$\frac{3}{16}$.
在矩形ABCD中,對角線AC,BD相交于點O,E為BO的中點,若$\overrightarrow{AE}=λ\overrightarrow{AB}+μ\overrightarrow{AD}$(λ,μ為實數),則λμ=$\frac{3}{16}$.查看答案和解析>>
科目:高中數學 來源: 題型:解答題
查看答案和解析>>
科目:高中數學 來源: 題型:填空題
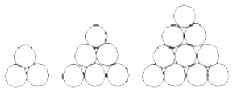 在德國不萊梅舉行的第48屆世乒賽期間,某商場櫥窗里用同樣的乒乓球堆成若干堆“正三棱錐”形的展品,其中第一堆只有一層,就一個乒乓球;第2、3、4、…堆最底層(第一層)分別按圖所示方式固定擺放.從第一層開始,每層的小球自然壘放在下一層之上,第n堆第n層就放一個乒乓球,以f(n)表示第n堆的乒乓球總數,則f(3)=10;f(n)=$\frac{1}{6}$n(n+1)(n+2)(答案用n表示).
在德國不萊梅舉行的第48屆世乒賽期間,某商場櫥窗里用同樣的乒乓球堆成若干堆“正三棱錐”形的展品,其中第一堆只有一層,就一個乒乓球;第2、3、4、…堆最底層(第一層)分別按圖所示方式固定擺放.從第一層開始,每層的小球自然壘放在下一層之上,第n堆第n層就放一個乒乓球,以f(n)表示第n堆的乒乓球總數,則f(3)=10;f(n)=$\frac{1}{6}$n(n+1)(n+2)(答案用n表示).查看答案和解析>>
科目:高中數學 來源: 題型:解答題
查看答案和解析>>
科目:高中數學 來源: 題型:填空題
查看答案和解析>>
科目:高中數學 來源: 題型:選擇題
| A. | (-∞,-3)∪(0,3) | B. | (-2,0)∪(3,+∞) | C. | (-3,3) | D. | (-∞,-3)∪(3,+∞) |
查看答案和解析>>
科目:高中數學 來源: 題型:解答題
 下表提供了某公司技術升級后生產A產品過程中記錄的產量x(噸)與相應的成本y(萬元)的幾組對照數據:
下表提供了某公司技術升級后生產A產品過程中記錄的產量x(噸)與相應的成本y(萬元)的幾組對照數據:| x | 3 | 4 | 5 | 6 |
| y | 2.5 | 3 | 4 | 4.5 |
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com