日日人人_亚洲美女在线视频_av手机在线播放_国产大片aaa_欧美中文日韩_午夜理伦三级

4．（文科）設(shè)函數(shù)$f（x）=\left\{\begin{array}{l}x，x＜1\\{x^3}-\frac{1}{x}+1，x≥1\end{array}\right.$，則$f（\frac{1}{f（2）}）$=$\frac{2}{17}$．

分析 利用分段函數(shù)的表達(dá)式，逐步求解函數(shù)值即可．

解答 解：設(shè)函數(shù)$f（x）=\left\{\begin{array}{l}x，x＜1\\{x^3}-\frac{1}{x}+1，x≥1\end{array}\right.$，
則f（2）=8-$\frac{1}{2}+1$=$\frac{17}{2}$．
$f（\frac{1}{f（2）}）$=f（$\frac{2}{17}$）=$\frac{2}{17}$．
故答案為：$\frac{2}{17}$．

點(diǎn)評 本題考查分段函數(shù)的應(yīng)用，函數(shù)值的求法，考查計(jì)算能力．

練習(xí)冊系列答案
相關(guān)習(xí)題

科目：高中數(shù)學(xué) 來源： 題型：解答題

14．在平面直角坐標(biāo)系xOy中，以原點(diǎn)O為極點(diǎn)，x軸的非負(fù)半軸為極軸，建立極坐標(biāo)系，若直線l的參數(shù)方程為$\left\{\begin{array}{l}{x=cosα}\\{y={y}_{0}+tsinα}\end{array}\right.$（t為參數(shù)，α為l的傾斜角），曲線E的極坐標(biāo)方程為ρ=4sinθ．射線θ=β，θ=β+$\frac{π}{4}$，θ=β-$\frac{π}{4}$與曲線E分別交于不同于極點(diǎn)的三點(diǎn)A、B、C．
（1）求證：|OB|+|OC|=$\sqrt{2}$|OA|；
（2）當(dāng)β=$\frac{7π}{12}$時，直線l過B、C兩點(diǎn)，求y0與α的值．

查看答案和解析>>

科目：高中數(shù)學(xué) 來源： 題型：解答題

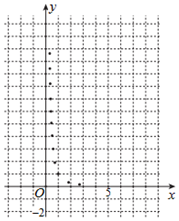15．某學(xué)生為了測試煤氣灶燒水如何節(jié)省煤氣的問題設(shè)計(jì)了一個實(shí)驗(yàn)，并獲得了煤氣開關(guān)旋鈕旋轉(zhuǎn)的弧度數(shù)x與燒開一壺水所用時間y的一組數(shù)據(jù)，且作了一定的數(shù)據(jù)處理（如表），得到了散點(diǎn)圖（如圖）．
$\bar x$$\bar y$$\bar w$$\sum_{i=1}^{10}{（{x_i}-\bar x）^2}$$\sum_{i=1}^{10}{（{w_i}-\bar w）^2}$$\sum_{i=1}^{10}（{x_i}-\bar x）（{y_i}-\bar y）$$\sum_{i=1}^{10}（{w_i}-\bar w）（{y_i}-\bar y）$
1.4720.60.782.350.81-19.316.2
表中${w_i}=\frac{1}{x_i^2}，\overline{w}=\frac{1}{10}\sum_{i=1}^{10}{w_i}$．
（1）根據(jù)散點(diǎn)圖判斷，y=a+bx與$y=c+\fracp9vv5xb5{x^2}$哪一個更適宜作燒水時間y關(guān)于開關(guān)旋鈕旋轉(zhuǎn)的弧度數(shù)x的回歸方程類型？（不必說明理由）
（2）根據(jù)判斷結(jié)果和表中數(shù)據(jù)，建立y關(guān)于x的回歸方程；
（3）若旋轉(zhuǎn)的弧度數(shù)x與單位時間內(nèi)煤氣輸出量t成正比，那么x為多少時，燒開一壺水最省煤氣？
附：對于一組數(shù)據(jù)（u1，v1），（u2，v2），（u3，v3），…，（un，vn），其回歸直線v=α+βu的斜率和截距的最小二乘估計(jì)分別為$\hat β=\frac{{\sum_{i=1}^n{（{v_i}-\bar v）（{u_i}-\bar u）}}}{{\sum_{i=1}^n{{{（{u_i}-\bar u）}^2}}}}，\hat α=\bar v-\hat β\bar u$．

查看答案和解析>>

科目：高中數(shù)學(xué) 來源： 題型：解答題

12．在銳角△ABC中，角A，B，C所對的邊分別為a，b，c，且$\overrightarrow{m}$=（$\sqrt{3}$，2sinA），$\overrightarrow{n}$=（c，a）若$\overrightarrow{m}∥\overrightarrow{n}$
（Ⅰ）求角C的大小；
（Ⅱ）若c=$\sqrt{7}$，且△ABC的面積為$\frac{3\sqrt{3}}{2}$，求a+b的值．

查看答案和解析>>

科目：高中數(shù)學(xué) 來源： 題型：解答題

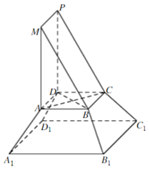19．《九章算術(shù)》是我國古代內(nèi)容極為豐富的數(shù)學(xué)名著，書中將底面為直角三角形，且側(cè)棱與底面垂直的棱柱稱為塹堵，將底面為矩形的棱臺稱為芻童．在如圖所示的塹堵ABM-DCP與芻童的組合體中AB=AD，A1B1=A1D1．棱臺體積公式：V=$\frac{1}{3}$（S′+$\sqrt{S′S}$+S）h，其中S′，S分別為棱臺上、下底面面積，h為棱臺高．
（Ⅰ）證明：直線BD⊥平面MAC；
（Ⅱ）若AB=1，A1D1=2，MA=$\sqrt{3}$，三棱錐A-A1B1D1的體積V=$\frac{2\sqrt{3}}{3}$，求該組合體的體積．

查看答案和解析>>

科目：高中數(shù)學(xué) 來源： 題型：解答題

9．設(shè)f（x）=xln x-ax2+（2a-1）x，a∈R．
（1）令g（x）=f′（x），求g（x）的單調(diào)區(qū)間；
（2）已知f（x）在x=1處取得極大值，求正實(shí)數(shù)a的取值范圍．

查看答案和解析>>

科目：高中數(shù)學(xué) 來源： 題型：填空題

16．若復(fù)數(shù)$\frac{2+ai}{1-i}（{a∈R}）$是純虛數(shù)（i是虛數(shù)單位），則復(fù)數(shù)z=a+（a-3）i在復(fù)平面內(nèi)對應(yīng)的點(diǎn)位于第四象限．

查看答案和解析>>

科目：高中數(shù)學(xué) 來源： 題型：選擇題

13．設(shè)a，b∈R，若a＞b，則（　　）
A．$\frac{1}{a}＜\frac{1}{b}$B．ac2＞bc2C．2-a＜2-bD．lga＞lgb

查看答案和解析>>

科目：高中數(shù)學(xué) 來源： 題型：選擇題

14．若{an}是等差數(shù)列，且a1=-1，公差為-3，則a8等于（　　）
A．-7B．-8C．-22D．27

查看答案和解析>>

同步練習(xí)冊答案
主站蜘蛛池模板： 日本精品免费 | 玖草资源 | 国产69精品99久久久久久宅男 | 国产精品视频专区 | 狠狠躁日日躁夜夜躁影院 | 黄色大片在线播放 | 色综合久久久久 | 久久国产精品久久久久久 | 国产成人精品一区二区三区四区 | 欧美成人性生活视频 | 天天干天天插 | 精品国产91久久 | 精品久久久影院 | 中文字幕不卡av | 黄色拍拍视频 | 日韩一区二区在线观看视频 | 91精品一区二区三区久久久久久 | 日本成人三级 | 中文字幕免费在线观看视频 | 欧美一区三区三区高中清蜜桃 | 97狠狠| 久久成人18免费网站 | 中文字幕久久精品 | 国产在线国偷精品产拍 | 日韩午夜精品视频 | 激情三区| 日韩成人免费视频 | 亚洲国产精品久久久久久 | 国产情侣免费视频 | 在线视频亚洲 | 久久网日本 | 成人网在线视频 | 国产小视频在线播放 | av大片在线观看 | youjizz欧美| 欧美日本免费一区二区三区 | 亚洲国产成人精品久久 | 国产suv精品一区二区6 | 网址你懂的| 成人精品一区 | 一级毛片aaaaaa免费看 |