
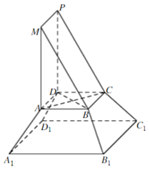
 《九章算術》是我國古代內容極為豐富的數學名著,書中將底面為直角三角形,且側棱與底面垂直的棱柱稱為塹堵,將底面為矩形的棱臺稱為芻童.在如圖所示的塹堵ABM-DCP與芻童的組合體中AB=AD,A1B1=A1D1.棱臺體積公式:V=$\frac{1}{3}$(S′+$\sqrt{S′S}$+S)h,其中S′,S分別為棱臺上、下底面面積,h為棱臺高.
《九章算術》是我國古代內容極為豐富的數學名著,書中將底面為直角三角形,且側棱與底面垂直的棱柱稱為塹堵,將底面為矩形的棱臺稱為芻童.在如圖所示的塹堵ABM-DCP與芻童的組合體中AB=AD,A1B1=A1D1.棱臺體積公式:V=$\frac{1}{3}$(S′+$\sqrt{S′S}$+S)h,其中S′,S分別為棱臺上、下底面面積,h為棱臺高.分析 (Ⅰ)證明AD⊥MA,推出MA⊥平面ABCD,得到MA⊥BD.結合BD⊥AC,證明BD⊥平面MAC.
(Ⅱ)設芻童ABCD-A1B1C1D1的高為h,利用幾何體的體積公式,轉化求解即可.
解答 解:(Ⅰ)證明:由題可知ABM-DCP是底面為直角三角形的直棱柱,
∴AD⊥平面MAB,
又MA?平面MAB,∴AD⊥MA,
又MA⊥AB,AD∩AB=A,AD,AB?平面ABCD,
∴MA⊥平面ABCD,
又BD?平面ABCD,
∴MA⊥BD.
又AB=AD,∴四邊形ABCD為正方形,
∴BD⊥AC,
又MA∩AC=A,MA,AC?平面MAC,
∴BD⊥平面MAC.…(6分)
(Ⅱ)設芻童ABCD-A1B1C1D1的高為h,
則三棱錐A-A1B1D1體積V=$\frac{1}{3}×\frac{1}{2}×2×2×h$=$\frac{2\sqrt{3}}{3}$,
∴h=$\sqrt{3}$,
故該組合體的體積為V=$\frac{1}{2}×1×\sqrt{3}×1+\frac{1}{3}({1}^{2}+{2}^{2}+\sqrt{{1}^{2}+{2}^{2}})×\sqrt{3}$=$\frac{17\sqrt{3}}{6}$.
點評 本題考查直線與平面垂直的判定定理的應用,組合體的體積的求法,考查計算能力.


 閱讀快車系列答案
閱讀快車系列答案科目:高中數學 來源: 題型:選擇題
| A. | a,b都為偶數 | B. | a,b不為偶數 | ||
| C. | a,b都不為偶數 | D. | a,b中有一個不為偶數 |
查看答案和解析>>
科目:高中數學 來源: 題型:解答題
查看答案和解析>>
科目:高中數學 來源: 題型:填空題
查看答案和解析>>
科目:高中數學 來源: 題型:填空題
查看答案和解析>>
科目:高中數學 來源: 題型:選擇題
| A. | π | B. | 4π | C. | 9π | D. | 16π |
查看答案和解析>>
科目:高中數學 來源: 題型:解答題
| ωx+φ | 0 | $\frac{π}{2}$ | π | $\frac{3π}{2}$ | 2π |
| x | $\frac{2π}{3}$ | $\frac{8π}{3}$ | |||
| Asin(ωx+φ) | 0 | 3 | 0 | -3 | 0 |
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com