
分析 (1)根據基本不等式即可求出函數的最值;
(2)根據對稱軸求出a=-1,分別求出f(x)max=1+c,g(x)min=2,即1+c≥2,解得即;
(3)把f(x+t)≤3x轉化為(x+t)2+2(x+t)≤3x,即h(x)=x2+(2t-1)x+t2+2t,在x∈[1,m]恒小于0問題,考查h(x)的圖象與性質,求出m的取值范圍.
解答 解:(1)∵x>0,∴$\frac{1}{x}>0$,
∴$x+\frac{1}{x}≥2$,當且僅當$x=\frac{1}{x}$,即x=1時“=”成立,即g(x)min=2,此時x=1.
(2)f(x)的對稱軸為x=1,
∴a=-1,
∴f(x)=-x2+2x+c,g(x)-f(x)=0至少有一個實根,
∴g(x)=f(x)至少有一個實根,
即g(x)與f(x)的圖象在(0,+∞)上至少有一個交點,f(x)=-(x-1)2+1+c,
∴f(x)max=1+c,g(x)min=2,
∴1+c≥2,∴c≥1,
∴c的取值范圍為[1,+∞).
(3)F(x)=x2-2x-c+4x+c=x2+2x,
∴F(x+t)=(x+t)2+2(x+t),
由已知存在實數t,對任意x∈[1,m],使(x+t)2+2(x+t)≤3x恒成立.
∴x2+(2t-1)x+t2+2t≤0.
令h(x)=x2+(2t-1)x+t2+2t,
∴$\left\{\begin{array}{l}h(1)≤0\\ h(m)≤0\end{array}\right.$,即$\left\{\begin{array}{l}{t^2}+4t≤0\\{t^2}+(2m+2)t+{m^2}-m≤0\end{array}\right.$,
轉化為存在t∈[-4,0],使t2+(2m+2)t+m2-m≤0成立.
令G(t)=t2+(2m+2)t+m2-m,
∴G(t)的對稱軸為t=-(m+1),
∵m>1,
∴-(m+1)<-2.
①當-4<-(m+1)<-2,即1<m<3時,
$G{(t)_{min}}=G(-m-1)={(-m-1)^2}+(2m+2)(-m-1)+{m^2}-m=-3m-1$,
∴$\left\{\begin{array}{l}1<m<3\\-3m-1≤0\end{array}\right.$,
∴1<m<3.
②當-(m+1)≤-4,即m≥3時,
$G{(t)_{min}}=G(-4)=16-8m-8+{m^2}-m={m^2}-9m+8$,
∴$\left\{\begin{array}{l}m≥3\\{m^2}-9m+8≤0\end{array}\right.$,
∴$\left\{\begin{array}{l}m≥3\\ 1≤m≤8\end{array}\right.$,
∴3≤m≤8.
綜上,實數m的取值范圍為(1,8].
點評 本題考查了二次函數在閉區間上的最值問題的應用,解題時應討論對稱軸在區間內還是在區間左側,還是區間右側,從而確定函數的最值.


科目:高中數學 來源: 題型:解答題
 已知x,y滿足$\left\{\begin{array}{l}{x-4y≤-3}\\{3x+5y≤25}\\{x≥1}\end{array}\right.$,z=2x-y
已知x,y滿足$\left\{\begin{array}{l}{x-4y≤-3}\\{3x+5y≤25}\\{x≥1}\end{array}\right.$,z=2x-y查看答案和解析>>
科目:高中數學 來源: 題型:解答題
查看答案和解析>>
科目:高中數學 來源: 題型:選擇題
| A. | $\frac{n}{3(2n+3)}$ | B. | $\frac{2n}{3(2n+3)}$ | C. | $\frac{n-1}{3(2n+1)}$ | D. | $\frac{n}{2n+1}$ |
查看答案和解析>>
科目:高中數學 來源: 題型:選擇題
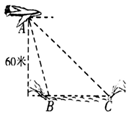 某人要利用無人機測量河流的寬度,如圖,從無人機A處測得正前方河流的兩岸B,C的俯角分別為75°,30°,此時無人機的高是60米,則河流的寬度BC等于( )
某人要利用無人機測量河流的寬度,如圖,從無人機A處測得正前方河流的兩岸B,C的俯角分別為75°,30°,此時無人機的高是60米,則河流的寬度BC等于( )| A. | $240\sqrt{3}$米 | B. | $180(\sqrt{2}-1)$米 | C. | $120(\sqrt{3}-1)$米 | D. | $30(\sqrt{3}+1)$米 |
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com