
分析 由已知向量的坐標結合向量共線可得tanx=$\frac{1}{3}$.
(1)利用三角函數的誘導公式化簡,進一步化弦為切求值;
(2)把分母看作sin2x+cos2x,分子分母同時除以cos2x,化為正切得答案.
解答 解:∵$\overrightarrow a∥\overrightarrow b$,∴sinx=$\frac{1}{3}cosx$,得tanx=$\frac{1}{3}$.
(1)$\frac{{sin(\frac{π}{2}+x)+cos(\frac{3π}{2}+x)}}{{cos(\frac{5π}{2}-x)+sin(\frac{7π}{2}-x)}}=\frac{cosx+sinx}{sinx-cosx}=\frac{1+tanx}{tanx-1}=\frac{{1+\frac{1}{3}}}{{\frac{1}{3}-1}}=-2$;
(2)${sin^2}x+sinxcosx=\frac{{{{sin}^2}x+sinxcosx}}{{{{sin}^2}x+{{cos}^2}x}}=\frac{{{{tan}^2}x+tanx}}{{{{tan}^2}x+1}}=\frac{{{{(\frac{1}{3})}^2}+\frac{1}{3}}}{{{{({\frac{1}{3}})}^2}+1}}=\frac{2}{5}$.
點評 本題考查平面向量的坐標運算,考查運用誘導公式化簡求值,是基礎題.


 陽光考場單元測試卷系列答案
陽光考場單元測試卷系列答案 名校聯盟沖刺卷系列答案
名校聯盟沖刺卷系列答案 名校提分一卷通系列答案
名校提分一卷通系列答案科目:高中數學 來源: 題型:解答題
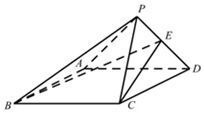 如圖,四棱錐P-ABCD中,底面ABCD邊長為4的正方形,PA=PD=2$\sqrt{2}$,平面PAD⊥平面PCD;
如圖,四棱錐P-ABCD中,底面ABCD邊長為4的正方形,PA=PD=2$\sqrt{2}$,平面PAD⊥平面PCD;查看答案和解析>>
科目:高中數學 來源: 題型:選擇題
| A. | 1 | B. | -1 | C. | $\frac{1}{2}$ | D. | $\sqrt{5}$ |
查看答案和解析>>
科目:高中數學 來源: 題型:解答題
查看答案和解析>>
科目:高中數學 來源: 題型:選擇題
| A. | [-1,2) | B. | [-1,2] | C. | [2,+∞) | D. | [-1,+∞) |
查看答案和解析>>
科目:高中數學 來源: 題型:填空題
查看答案和解析>>
科目:高中數學 來源: 題型:解答題
查看答案和解析>>
科目:高中數學 來源: 題型:解答題
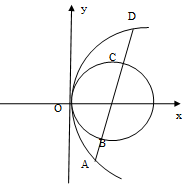 如右圖拋物線頂點在原點,圓(x-2)2+y2=22的圓心恰是拋物線的焦點,
如右圖拋物線頂點在原點,圓(x-2)2+y2=22的圓心恰是拋物線的焦點,查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com