
| A. | $\frac{{2+\sqrt{3}}}{7}$ | B. | $\frac{{3+\sqrt{3}}}{7}$ | C. | $\frac{{3+2\sqrt{3}}}{7}$ | D. | $\frac{{4+2\sqrt{3}}}{7}$ |
分析 由已知可得$\overrightarrow{OM}$=$\frac{1}{7}$$\overrightarrow{OA}$+$\frac{3}{7}$$\overrightarrow{OB}$,若過M作動直線l分別交線段AC,BD于E,F兩點,若$\overrightarrow{OE}$=λ$\overrightarrow{OA}$,$\overrightarrow{OF}$=μ$\overrightarrow{OB}$,(λ,μ>0),則$\frac{1}{λ}$+$\frac{3}{μ}$=7,再由基本不等式可得答案.
解答 解:由A,M,D三點共線可得存在實數t使得
$\overrightarrow{OM}$=t$\overrightarrow{OA}$+(1-t)$\overrightarrow{OD}$=t$\overrightarrow{OA}$+$\frac{1}{2}$(1-t)$\overrightarrow{OB}$,
同理由C,M,B三點共線可得存在實數m使得
$\overrightarrow{OM}$=m$\overrightarrow{OB}$+(1-m)$\overrightarrow{OC}$=$\frac{1}{4}$(1-m)$\overrightarrow{OA}$+m$\overrightarrow{OB}$,
∴$\left\{\begin{array}{l}t=\frac{1}{4}(1-m)\\ \frac{1}{2}(1-t)=m\end{array}\right.$,
解得$\left\{\begin{array}{l}m=\frac{3}{7}\\ t=\frac{1}{7}\end{array}\right.$,
∴$\overrightarrow{OM}$=$\frac{1}{7}$$\overrightarrow{OA}$+$\frac{3}{7}$$\overrightarrow{OB}$,
設$\overrightarrow{OM}$=x$\overrightarrow{OE}$+y$\overrightarrow{OF}$=xλ$\overrightarrow{OA}$+yμ$\overrightarrow{OB}$,
則$\left\{\begin{array}{l}xλ=\frac{1}{7}\\ yμ=\frac{3}{7}\end{array}\right.$,
即$\left\{\begin{array}{l}7x=\frac{1}{λ}\\ 7y=\frac{3}{μ}\end{array}\right.$,
即$\frac{1}{λ}$+$\frac{3}{μ}$=7,
故λ+μ=$\frac{1}{7}$(λ+μ)($\frac{1}{λ}$+$\frac{3}{μ}$)=$\frac{1}{7}$(1+3+$\frac{μ}{λ}$+$\frac{3λ}{μ}$)≥$\frac{4+2\sqrt{3}}{7}$,
即λ+μ的最小值為$\frac{4+2\sqrt{3}}{7}$,
故選:D
點評 本題考查的知識點是平面向量在幾何中的應用,三點共線的充要條件,基本不等式的應用,難度中檔.


 黃岡360度定制密卷系列答案
黃岡360度定制密卷系列答案 陽光考場單元測試卷系列答案
陽光考場單元測試卷系列答案 名校聯盟沖刺卷系列答案
名校聯盟沖刺卷系列答案 名校提分一卷通系列答案
名校提分一卷通系列答案科目:高中數學 來源: 題型:填空題
查看答案和解析>>
科目:高中數學 來源: 題型:選擇題
| A. | 9 | B. | 10 | C. | 9 或 10 | D. | 10 或 11 |
查看答案和解析>>
科目:高中數學 來源: 題型:選擇題
| A. | {-2,-1,0} | B. | {-1,0,1,2} | C. | {-2,-1} | D. | {-1,0,1} |
查看答案和解析>>
科目:高中數學 來源: 題型:解答題
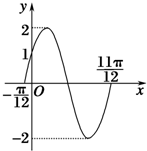 若f(x)=Asin(ωx+θ)(A>0,ω>0,|θ|<$\frac{π}{2}$)的圖象如圖所示,
若f(x)=Asin(ωx+θ)(A>0,ω>0,|θ|<$\frac{π}{2}$)的圖象如圖所示,查看答案和解析>>
科目:高中數學 來源: 題型:選擇題
| A. | 8 | B. | 0 | C. | 2 | D. | -2 |
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com