Question

3．在△ABC中，BC=4，AC、AB邊上的中線長之和等于9．
（1）求△ABC重心M的軌跡方程；
（2）求頂點A的軌跡方程．

Answer 1

分析 （1）由已知得△ABC重心M在以B、C為兩個焦點的橢圓，由此能求出△ABC重心M的軌跡方程．
（2）利用代入法，即可求頂點A的軌跡方程．

解答 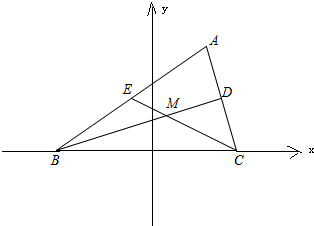解：（1）如圖所示，以線段BC所在直線為x軸、線段BC的中垂線為y軸建立直角坐標系…（2分）
設M為△ABC的重心，BD是AC邊上的中線，CE是AB邊上的中線，由重心的性質知|BM|=$\frac{2}{3}$|BD|，|CM|=$\frac{2}{3}$|CE|，于是|MB|+|MC|=$\frac{2}{3}$|BD|+$\frac{2}{3}$|CE|=6…（4分）
根據橢圓的定義知，點M的軌跡是以B、C為焦點的橢圓．2a=6，2c=4，
∴a=3，b=$\sqrt{5}$，…（5分）
故所求的橢圓方程為$\frac{{x}^{2}}{9}+\frac{{y}^{2}}{5}$=1（y≠0）…（6分）
（2）設A（x，y），則M（$\frac{1}{3}$x，$\frac{1}{3}y$），代入$\frac{{x}^{2}}{9}+\frac{{y}^{2}}{5}$=1（y≠0），
可得出頂點A的軌跡方程為$\frac{{x}^{2}}{81}+\frac{{y}^{2}}{45}$=1（y≠0）…（12分）

點評 本題考查點的軌跡方程的求法，考查代入法，解題時要認真審題，注意橢圓定義的合理運用．