
分析 (I)取n=2,3可得a2,a3,由an=$\frac{n}{n-1}$an-1+2n•3n-2(n≥2,n∈N*),可得:$\frac{{a}_{n}}{n}$-$\frac{{a}_{n-1}}{n-1}$=2×3n-2.利用累加求和方法即可得出an;
(II)求出bn,得出Sn,從而得出S${\;}_{{2}^{n}}$,分別取n=1,2,3,比較S${\;}_{{2}^{n}}$與n的大小,歸納得出結論,利用數(shù)學歸納法給出證明.
解答 解:(I)a2=2a1+4=6,a3=$\frac{3}{2}$a2+18=27.
∵an=$\frac{n}{n-1}$an-1+2n•3n-2(n≥2,n∈N*).
∴$\frac{{a}_{n}}{n}$-$\frac{{a}_{n-1}}{n-1}$=2×3n-2,
$\frac{{a}_{n-1}}{n-1}$-$\frac{{a}_{n-2}}{n-2}$=2×3n-3,
…
$\frac{{a}_{2}}{2}$-$\frac{{a}_{1}}{1}$=2×30,
以上各式相加得:$\frac{{a}_{n}}{n}$-a1=2×(3n-2+3n-3+…+30)=2×$\frac{{3}^{n-1}-1}{3-1}$=3n-1-1,
∴$\frac{{a}_{n}}{n}$=3n-1,
∴an=n•3n-1.
(II)bn=$\frac{{3}^{n-1}}{{a}_{n}}$=$\frac{1}{n}$,
數(shù)列{bn}的前n項和為Sn=$1+\frac{1}{2}+\frac{1}{3}$+…+$\frac{1}{n}$.
則S${\;}_{{2}^{n}}$=$1+\frac{1}{2}+\frac{1}{3}$+…+$\frac{1}{n}$+$\frac{1}{n+1}$+…+$\frac{1}{{2}^{n}-1}$+$\frac{1}{{2}^{n}}$.
n=1,S2=1+$\frac{1}{2}$>1;
n=2時,${S}_{{2}^{2}}$=$1+\frac{1}{2}+\frac{1}{3}$+$\frac{1}{4}$>2.
n=3時,${S}_{{2}^{3}}$=$1+\frac{1}{2}+\frac{1}{3}$+…+$\frac{1}{{2}^{3}}$<3.
猜想:當n≥3時,S${\;}_{{2}^{n}}$<n,
下面用數(shù)學歸納法給出證明,
(1)顯然n=3時,S${\;}_{{2}^{3}}$<3,
(2)假設n=k(k≥3)時,${S}_{{2}^{n}}$<n.
即1+$\frac{1}{2}+\frac{1}{3}$+…+$\frac{1}{{2}^{k}}$<k,
則1+$\frac{1}{2}+\frac{1}{3}$+…+$\frac{1}{{2}^{k}}$+$\frac{1}{{2}^{k}+1}$+$\frac{1}{{2}^{k}+2}$+…+$\frac{1}{{2}^{k+1}}$<k+$\frac{1}{{2}^{k}+1}$+$\frac{1}{{2}^{k}+2}$+…+$\frac{1}{{2}^{k+1}}$
<k+$\frac{1}{{2}^{k}+1}$+$\frac{1}{{2}^{k}+1}$+$\frac{1}{{2}^{k}+1}$+…$\frac{1}{{2}^{k}+1}$=k+$\frac{{2}^{k}}{{2}^{k}+1}$<k+1,
即S${\;}_{{2}^{k+1}}$<k+1,
∴當n=k+1時,猜想也成立.
綜上可得:n=1,2時,${S}_{{2}^{n}}$>n;n≥3時,${S}_{{2}^{n}}$<n.
點評 本題考查了數(shù)列通項公式的求法,數(shù)學歸納法,屬于中檔題.


 陽光課堂課時優(yōu)化作業(yè)系列答案
陽光課堂課時優(yōu)化作業(yè)系列答案科目:高中數(shù)學 來源: 題型:選擇題
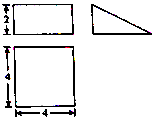
| A. | 32+8$\sqrt{5}$ | B. | 36π | C. | 18π | D. | $\frac{40\sqrt{10}}{3}$π |
查看答案和解析>>
科目:高中數(shù)學 來源: 題型:解答題
查看答案和解析>>
科目:高中數(shù)學 來源: 題型:解答題
查看答案和解析>>
科目:高中數(shù)學 來源: 題型:解答題
查看答案和解析>>
科目:高中數(shù)學 來源: 題型:解答題
查看答案和解析>>
科目:高中數(shù)學 來源: 題型:選擇題
| A. | {3,5,7} | B. | {3,7} | C. | {4,5,6} | D. | {5} |
查看答案和解析>>
湖北省互聯(lián)網違法和不良信息舉報平臺 | 網上有害信息舉報專區(qū) | 電信詐騙舉報專區(qū) | 涉歷史虛無主義有害信息舉報專區(qū) | 涉企侵權舉報專區(qū)
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com