
| A. | (0,$\frac{3}{4}$) | B. | ($\frac{5}{12}$,$\frac{3}{4}$] | C. | ($\frac{3}{4}$,1] | D. | ($\frac{3}{4}$,+∞] |
分析 直線方程變形,判斷出直線過定點;求出特殊位置k的值,即可求出滿足題意的k的范圍.
解答 解:曲線y=$\sqrt{4-{x}^{2}}$即x2+y2=4,(y≥0)
表示一個以(0,0)為圓心,以2為半徑的位于x軸上方的半圓,如圖所示:
直線kx-y-2k+4=0即y=k(x-2)+4,表示恒過點A(2,4)斜率為k的直線
B(2-,0)時,kAB=1,
∵$\frac{|-2k+4|}{\sqrt{1+{k}^{2}}}$=2解得k=$\frac{3}{4}$
∴要使直線與半圓有兩個不同的交點,k的取值范圍是($\frac{3}{4}$,1].
故選C.
點評 解決直線與二次曲線的交點問題,常先化簡曲線的方程,一定要注意做到同解變形,數形結合解決參數的范圍問題.


 同步練習河南大學出版社系列答案
同步練習河南大學出版社系列答案 同步練習西南師范大學出版社系列答案
同步練習西南師范大學出版社系列答案 補充習題江蘇系列答案
補充習題江蘇系列答案 學練快車道口算心算速算天天練系列答案
學練快車道口算心算速算天天練系列答案科目:高中數學 來源: 題型:選擇題
| A. | 3 | B. | 12 | C. | $2\sqrt{2}$ | D. | $8\sqrt{2}$ |
查看答案和解析>>
科目:高中數學 來源: 題型:選擇題
| A. | m>0或m<-4 | B. | -4<m<0 | C. | -4<m≤0 | D. | 0<m<4 |
查看答案和解析>>
科目:高中數學 來源: 題型:選擇題
| A. | 一定是銳角三角形 | B. | 一定是直角三角形 | ||
| C. | 一定是鈍角三角形 | D. | 是銳角或直角三角形 |
查看答案和解析>>
科目:高中數學 來源: 題型:選擇題
| A. | p∧q | B. | (¬p)∧q | C. | p∧(¬q) | D. | (¬p)∧(¬q) |
查看答案和解析>>
科目:高中數學 來源: 題型:解答題
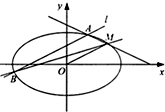 如圖,橢圓C:$\frac{{x}^{2}}{{a}^{2}}$+$\frac{{y}^{2}}{{b}^{2}}$=1(a>b>0)的虛軸長為2$\sqrt{2}$,點M(2,1)在C上,平行于OM的直線l交橢圓C于不同的兩點A,B.
如圖,橢圓C:$\frac{{x}^{2}}{{a}^{2}}$+$\frac{{y}^{2}}{{b}^{2}}$=1(a>b>0)的虛軸長為2$\sqrt{2}$,點M(2,1)在C上,平行于OM的直線l交橢圓C于不同的兩點A,B.查看答案和解析>>
科目:高中數學 來源: 題型:解答題
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com