
分析 (1)不等式等價于$\left\{\begin{array}{l}{(x+2)(x-3)≤0}\\{x-3≠0}\end{array}\right.$,即可解不等式;
(2)不等式等價于3x-1≥7或3x-1≤-7,即可解不等式.
解答 解:(1)不等式等價于$\left\{\begin{array}{l}{(x+2)(x-3)≤0}\\{x-3≠0}\end{array}\right.$,解得-2≤x<3,
∴不等式的解集為[-2,3);
(2)不等式等價于3x-1≥7或3x-1≤-7,
解得x≤-2或x≥$\frac{8}{3}$,
∴不等式的解集為{x|x≤-2或x≥$\frac{8}{3}$}.
點評 本題考查不等式的解法,考查學生的計算能力,正確等價變形是關鍵.


科目:高中數學 來源: 題型:填空題
查看答案和解析>>
科目:高中數學 來源: 題型:選擇題
| A. | 函數g(x)的最小正周期為5π | B. | 函數g(x)的圖象關于直線x=$\frac{π}{4}$對稱 | ||
| C. | 函數g(x)在區間[π,2π]上增函數 | D. | 函數g(x)是奇函數 |
查看答案和解析>>
科目:高中數學 來源: 題型:填空題
查看答案和解析>>
科目:高中數學 來源: 題型:選擇題
| A. | y=sinxcosx | B. | y=cos2x | C. | y=|tanx| | D. | $y=sin(2x+\frac{π}{3})$ |
查看答案和解析>>
科目:高中數學 來源: 題型:選擇題
| A. | $[{\frac{7}{4},+∞})$ | B. | [2,+∞) | C. | [1,+∞) | D. | (-∞,-1] |
查看答案和解析>>
科目:高中數學 來源: 題型:選擇題
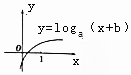 已知函數f(x)=loga(x+b)(a,b為常數)的圖象如圖所示,則函數g(x)=b${\;}^{{x^2}-4x}}$在[0,5]上的最大值是( )
已知函數f(x)=loga(x+b)(a,b為常數)的圖象如圖所示,則函數g(x)=b${\;}^{{x^2}-4x}}$在[0,5]上的最大值是( )| A. | $\frac{1}{b^4}$ | B. | $\frac{1}{b^5}$ | C. | b4 | D. | b5 |
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com