
分析 (1)運用奇函數的定義和單調性的定義,將b換為-b,即可得證;
(2)由f(x)在[-1,1]遞增,可得不等式組,注意定義域,解不等式即可得到所求解集;
(3)由題意可得由m<0,即m2-2≤f(x)-2mx的最小值,運用單調性不等式右邊函數的最小值,再解m的不等式即可得到所求范圍.
解答 解:(1)證明:∵f(x)是定義在[-1,1]上奇函數,
∴f(-x)=-f(x).
∵對任意的a,b∈[-1,1],當a+b≠0時,都有$\frac{f(a)+f(b)}{a+b}$>0,
∴-b∈[-1,1],$\frac{f(a)+f(-b)}{a+(-b)}$>0.
∴$\frac{f(a)-f(b)}{a-b}$>0,
∴當a>b時,f(a)>f(b),
當a<b時,f(a)<f(b),
∴由a、b的任意性知:f(x)在區間[-1,1]上單調遞增;
(2)由f(x)在[-1,1]遞增,
f(x-$\frac{1}{2}$)<f($\frac{1}{4}$-x),
可得$\left\{\begin{array}{l}{-1≤x-\frac{1}{2}≤1}\\{-1≤\frac{1}{4}-x≤1}\\{x-\frac{1}{2}<\frac{1}{4}-x}\end{array}\right.$,即$\left\{\begin{array}{l}{-\frac{1}{2}≤x≤\frac{3}{2}}\\{-\frac{3}{4}≤x≤\frac{5}{4}}\\{x<\frac{3}{8}}\end{array}\right.$,
可得-$\frac{1}{2}$≤x<$\frac{3}{8}$.
則原不等式解集為[-$\frac{1}{2}$,$\frac{3}{8}$);
(3)對于任意x∈[-1,1],m2+2mx-2≤f(x)恒成立,
由m<0,即m2-2≤f(x)-2mx的最小值,
由f(x)在[-1,1]遞增,2mx在[-1,1]遞減,
且f(1)=1,f(-1)=-f(1)=-1,
可得f(x)-2mx的最小值為-1+2m,
即有m2-2≤2m-1,即m2-2m-1≤0,
解得1-$\sqrt{2}$≤m<0.
則負數m的取值范圍為[1-$\sqrt{2}$,0).
點評 本題考查函數的奇偶性和單調性的運用,考查不等式恒成立問題的解法,考查化簡整理的運算能力,屬于中檔題.


科目:高中數學 來源: 題型:解答題
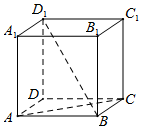 如圖,在正方體ABCD-A1B1C1D1中.
如圖,在正方體ABCD-A1B1C1D1中.查看答案和解析>>
科目:高中數學 來源: 題型:解答題
查看答案和解析>>
科目:高中數學 來源: 題型:解答題
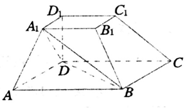 如圖所示,在四棱臺ABCD-A1B1C1D1中,底面ABCD是平行四邊形,DD1⊥平面ABCD,AB=2AD,AD=A1B1,∠BAD=60°.
如圖所示,在四棱臺ABCD-A1B1C1D1中,底面ABCD是平行四邊形,DD1⊥平面ABCD,AB=2AD,AD=A1B1,∠BAD=60°.查看答案和解析>>
科目:高中數學 來源: 題型:填空題
查看答案和解析>>
科目:高中數學 來源: 題型:選擇題
| A. | 命題“若x>1,則x2>1”的否命題 | B. | 命題“若x>y,則x>|y|”的逆命題 | ||
| C. | 命題“若x=1,則x2+x-2=0”的否命題 | D. | 命題“若x2≥1,則x≥1”的逆否命題 |
查看答案和解析>>
科目:高中數學 來源: 題型:選擇題
| A. | 三角形的邊長與面積之間的關系 | |
| B. | 等邊三角形的邊長與面積之間的關系 | |
| C. | 四邊形的邊長與面積之間的關 | |
| D. | 菱形的邊長與面積之間的關 |
查看答案和解析>>
科目:高中數學 來源: 題型:填空題
查看答案和解析>>
科目:高中數學 來源: 題型:解答題
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com