Question

12．已知b≥a＞0，若存在實數x，y滿足0≤x≤a，0≤y≤b，（x-a）²+（y-b）²=x²+b²=a²+y²，則$\frac{b}{a}$的最大值為$\frac{2\sqrt{3}}{3}$．

Answer 1

分析 設A（0，b），B（x，0），C（a，b-y），由x-a）²+（y-b）²=x²+b²=a²+y²
得△ABC為等邊△，設△ABC邊長為m，∠OAB=θ，（0$≤θ≤\frac{π}{6}$）
過C作CH⊥x軸與H，則∠ACH=θ-$\frac{π}{6}$，a=mcos（$θ-\frac{π}{6}$），b=mcosθ即可求解．

解答 解：如圖設A（0，b），B（x，0），C（a，b-y）
∵（x-a）²+（y-b）²=x²+b²=a²+y²
∴△ABC為等邊△，設△ABC邊長為m，∠OAB=θ，（0$≤θ≤\frac{π}{6}$）
過C作CH⊥x軸與H，則∠ACH=θ-$\frac{π}{6}$，∴$a=mcos（θ-\frac{π}{6}）$
b=mcosθ
∴$\frac{b}{a}=\frac{cosθ}{cos（θ-\frac{π}{6}）}=\frac{1}{\frac{\sqrt{3}}{2}+\frac{1}{2}tanθ}$
∴當θ=0時，$（\frac{b}{a}）_{nax}=\frac{2\sqrt{3}}{3}$
故答案為：$\frac{2\sqrt{3}}{3}$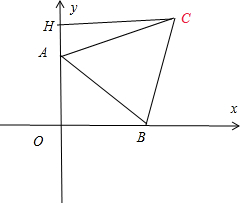

點評 本題考查了通過解析法處理最值問題，考查了轉化思想、運算能力，屬于中檔題．