
分析 (1)根據數列:2,3,6,m(m>6)是“兌換系數”為a的“兌換數列”所以a-m,a-6,a-3,a-2也是該數列的項,且a-m<a-6<a-3<a-2,由此可求m和a的值;
(2)由“兌換數列”的定義證明數列{bn}是“兌換數列”,即證對數列{bn}中的任意一項bi(1≤i≤n0),a-bi=b1+(n0-i)d=bn0+1-i∈{bn},從而可求數列{bn}所有項之和;
(3)假設存在這樣的等比數列{cn},設它的公比為q(q>1),可知數列{cn}必為有窮數列,不妨設項數為n項,則ci+cn+1-i=a(1≤i≤n),再分類討論,即可得到結論.
解答 (1)解:因為2,3,6,m(m>6)是“兌換系數”為a的“兌換數列”
所以a-m,a-6,a-3,a-2也是該數列的項,且a-m<a-6<a-3<a-2,
故a-m=2,a-6=3,即a=9,m=7.
(2)證明:設數列{bn}的公差為d,
因為數列{bn}是項數為n0項的有窮等差數列
若b1≤b2≤b3≤…≤b${\;}_{{n}_{0}}$,則a-b1≥a-b2≥a-b3≥…≥a-b${\;}_{{n}_{0}}$,
即對數列{bn}中的任意一項bi(1≤i≤n0),a-bi=b1+(n0-i)d=b${\;}_{{n}_{0}}$+1-i∈{bn}
同理可得:b1≥b2≥b3≥…≥b${\;}_{{n}_{0}}$,a-bi=b1+(n0-i)d=b${\;}_{{n}_{0}}$+1-i∈{bn}也成立,
由“兌換數列”的定義可知,數列{bn}是“兌換數列”;
又因為數列{bn}所有項之和是B,所以B=$\frac{({b}_{1}+{b}_{{n}_{0}})•{n}_{0}}{2}$=$\frac{a{n}_{0}}{2}$,即a=$\frac{2B}{{n}_{0}}$;
(3)解:假設存在這樣的等比數列{cn},設它的公比為q(q>1),
因為數列{cn}為遞增數列,所以c1<c2<c3<…<cn,則a-c1>a-c2>a-c3>…>a-cn,
又因為數列{cn}為“兌換數列”,則a-ci∈{cn},所以a-ci是正整數
故數列{cn}必為有窮數列,不妨設項數為n項,則ci+cn+1-i=a(1≤i≤n)
①若n=3,則有c1+c3=a,c2=$\frac{a}{2}$,又c22=c1c3,由此得q=1,與q>1矛盾
②若n≥4,由c1+cn=c2+cn-1,得c1-c1q+c1qn-1-c1qn-2=0
即(q-1)(1-qn-2)=0,故q=1,與q>1矛盾;
綜合①②得,不存在滿足條件的數列{cn}.
點評 本題考查新定義,考查學生的閱讀能力,考查學生分析解決問題的能力,屬于中檔題.


科目:高中數學 來源: 題型:選擇題
| A. | a>b>c | B. | b>a>c | C. | c>b>a | D. | a>c>b |
查看答案和解析>>
科目:高中數學 來源: 題型:解答題
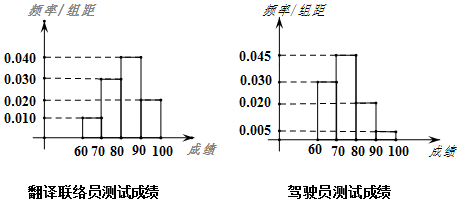
| P(K2≥k0) | 0.10 | 0.05 | 0.010 | 0.001 |
| k0 | 2.706 | 3.841 | 6.635 | 10.828 |
查看答案和解析>>
科目:高中數學 來源: 題型:解答題
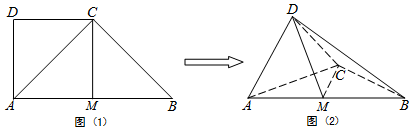
查看答案和解析>>
科目:高中數學 來源: 題型:填空題
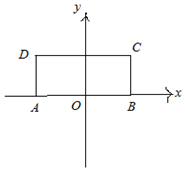 如圖,在矩形ABCD中,AB=12,BC=5,以A、B為焦點的雙曲線$M:\frac{x^2}{a^2}-\frac{y^2}{b^2}=1$恰好過C、D兩點,則雙曲線M的標準方程為$\frac{x^2}{16}-\frac{y^2}{20}=1$.
如圖,在矩形ABCD中,AB=12,BC=5,以A、B為焦點的雙曲線$M:\frac{x^2}{a^2}-\frac{y^2}{b^2}=1$恰好過C、D兩點,則雙曲線M的標準方程為$\frac{x^2}{16}-\frac{y^2}{20}=1$.查看答案和解析>>
科目:高中數學 來源: 題型:選擇題
| A. | $\frac{25}{6}$ | B. | $\frac{8}{3}$ | C. | $\frac{11}{3}$ | D. | 4 |
查看答案和解析>>
科目:高中數學 來源: 題型:選擇題
| A. | ¬q | B. | (¬p)∨(¬q) | C. | p∧q | D. | p∧(¬q) |
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com