
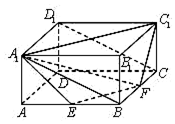
 如圖,在長方體ABCD-A1B1C1D1中,AA1=1,AB=AD=2,E,F分別是棱AB,BC的中點,證明A1,C1,F,E四點共面,并求點B到平面A1EF的距離.
如圖,在長方體ABCD-A1B1C1D1中,AA1=1,AB=AD=2,E,F分別是棱AB,BC的中點,證明A1,C1,F,E四點共面,并求點B到平面A1EF的距離. 分析 連接AC,因為E,F分別是AB,BC的中點,可得EF∥A1C1,即A1、C1、F、E四點共面.
設點B到平面A1EF的距離為d,
由V${\;}_{B-{A}_{1}EF}$=V${\;}_{F-{A}_{1}EB}$,⇒$\frac{1}{3}×{s}_{{△A}_{1}EF}×d=\frac{1}{3}{s}_{△{A}_{1}EB}×FB$,可得點B到平面A1EF的距離
解答 解:連接AC,因為E,F分別是AB,BC的中點,所以EF是△ABC的中位線,所以EF∥AC.由長方體的性質知AC∥A1C1,
所以EF∥A1C1,所以A1、C1、F、E四點共面.
設點B到平面A1EF的距離為d,
∵V${\;}_{B-{A}_{1}EF}$=V${\;}_{F-{A}_{1}EB}$,⇒$\frac{1}{3}×{s}_{{△A}_{1}EF}×d=\frac{1}{3}{s}_{△{A}_{1}EB}×FB$
∵${A}_{1}E=EF=\sqrt{2}$,${A}_{1}F=\sqrt{A{A}^{2}+A{B}^{2}+B{F}^{2}}$=$\sqrt{6}$,∴${s}_{△{A}_{1}EF}=\frac{\sqrt{3}}{2}$
${s}_{△{A}_{1}EB}=\frac{1}{2}{s}_{△{A}_{1}AB}=\frac{1}{2}$
∴$d=\frac{\sqrt{3}}{3}$,∴點B到平面A1EF的距離d=$\frac{\sqrt{3}}{3}$
點評 本題考查了空間四點共面的判定,等體積法求點面距離,屬于中檔題


 智趣寒假作業云南科技出版社系列答案
智趣寒假作業云南科技出版社系列答案科目:高中數學 來源: 題型:選擇題
| A. | 2 | B. | $\sqrt{3}$ | C. | $\sqrt{2}$ | D. | 1 |
查看答案和解析>>
科目:高中數學 來源: 題型:選擇題
| A. | 729 | B. | 243 | C. | 64 | D. | 1 |
查看答案和解析>>
科目:高中數學 來源: 題型:填空題
| 死亡 | 存活 | 總計 | |
| 第一種劑量 | 14 | 11 | 25 |
| 第二種劑量 | 6 | 19 | 25 |
| 總計 | 20 | 30 | 50 |
查看答案和解析>>
科目:高中數學 來源: 題型:解答題
查看答案和解析>>
科目:高中數學 來源: 題型:選擇題
| A. | -$\frac{21}{2}$ | B. | -$\frac{5}{4}$ | C. | -1 | D. | -$\frac{15}{8}$ |
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com