
| A. | 2 | B. | $\sqrt{3}$ | C. | $\sqrt{2}$ | D. | 1 |
分析 運用向量的數量積的定義可得$<\overrightarrow a,\overrightarrow b>={135°}$,不妨設$\overrightarrow a=(1,1)$,$\overrightarrow b=(-1,0)$,設$\overrightarrow c=(x,y)$,運用向量的數量積的加減和數量積的坐標表示,計算即可得到所求最大值.
解答 解:根據題意,向量$|{\overrightarrow a}|=\sqrt{2},|{\overrightarrow b}|=1,|{\overrightarrow c}|=\sqrt{3}$,且$\overrightarrow a•\overrightarrow b=-1$,
可得cos<$\overrightarrow{a}$,$\overrightarrow{b}$>=$\frac{\overrightarrow{a}•\overrightarrow{b}}{|\overrightarrow{a}|•|\overrightarrow{b}|}$=$\frac{-1}{\sqrt{2}}$,
由于0°≤<$\overrightarrow{a}$,$\overrightarrow{b}$>≤180°,
即有$<\overrightarrow a,\overrightarrow b>={135°}$,不妨設$\overrightarrow a=(1,1)$,$\overrightarrow b=(-1,0)$,
設$\overrightarrow c=(x,y)$,且x2+y2=3,易知$|y|≤\sqrt{3}$
則$\overrightarrow a•\overrightarrow c+\overrightarrow b•\overrightarrow c=(\overrightarrow a+\overrightarrow b)•\overrightarrow c=(0,1)•(x,y)=y≤\sqrt{3}$.
當x=0,y=$\sqrt{3}$時,取得最大值$\sqrt{3}$.
故選:B.
點評 本題考查向量的數量積的定義和性質,以及向量的數量積的坐標表示,以及不等式的性質,屬于中檔題.


 千里馬走向假期期末仿真試卷寒假系列答案
千里馬走向假期期末仿真試卷寒假系列答案科目:高中數學 來源: 題型:填空題
查看答案和解析>>
科目:高中數學 來源: 題型:選擇題
| A. | 0 | B. | 1 | C. | 2 | D. | 3 |
查看答案和解析>>
科目:高中數學 來源: 題型:解答題
查看答案和解析>>
科目:高中數學 來源: 題型:選擇題
| A. | p1,p2 | B. | p3,p4 | C. | p2,p3 | D. | p1,p4 |
查看答案和解析>>
科目:高中數學 來源: 題型:解答題
查看答案和解析>>
科目:高中數學 來源: 題型:填空題
查看答案和解析>>
科目:高中數學 來源: 題型:解答題
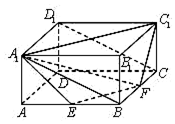 如圖,在長方體ABCD-A1B1C1D1中,AA1=1,AB=AD=2,E,F分別是棱AB,BC的中點,證明A1,C1,F,E四點共面,并求點B到平面A1EF的距離.
如圖,在長方體ABCD-A1B1C1D1中,AA1=1,AB=AD=2,E,F分別是棱AB,BC的中點,證明A1,C1,F,E四點共面,并求點B到平面A1EF的距離.查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com