
分析 (1)根據平面向量數量積的定義,計算即可;
(2)根據兩向量垂直,數量積為0,列出方程求$\overrightarrow{a}$與$\overrightarrow{b}$夾角的余弦值和夾角的大小.
解答 解:(1)|$\overrightarrow{a}$|=1,|$\overrightarrow{b}$|=$\sqrt{2}$,$\overrightarrow{a}$與$\overrightarrow{b}$的夾角為$\frac{3π}{4}$時,
$\overrightarrow{a}$•$\overrightarrow{b}$=1×$\sqrt{2}$×cos$\frac{3π}{4}$=-1,
∴($\overrightarrow{a}$+$\overrightarrow{b}$)•($\overrightarrow{a}$+$\overrightarrow{b}$)=${\overrightarrow{a}}^{2}$+2$\overrightarrow{a}$•$\overrightarrow{b}$+${\overrightarrow{b}}^{2}$=1-1+2=2;
(2)若$\overrightarrow{a}$-$\overrightarrow{b}$ 與$\overrightarrow{a}$垂直,則($\overrightarrow{a}$-$\overrightarrow{b}$)•$\overrightarrow{a}$=0,
∴${\overrightarrow{a}}^{2}$-$\overrightarrow{a}$•$\overrightarrow{b}$=0,
即1-1×$\sqrt{2}$×cosθ=0,
解得cosθ=$\frac{\sqrt{2}}{2}$;
又θ∈[0,π],
∴θ=$\frac{π}{4}$,
即$\overrightarrow{a}$與$\overrightarrow{b}$的夾角為$\frac{π}{4}$.
點評 本題考查了平面向量數量積的定義與運算問題,是基礎題.


科目:高中數學 來源: 題型:解答題
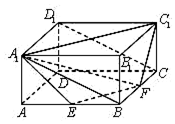 如圖,在長方體ABCD-A1B1C1D1中,AA1=1,AB=AD=2,E,F分別是棱AB,BC的中點,證明A1,C1,F,E四點共面,并求點B到平面A1EF的距離.
如圖,在長方體ABCD-A1B1C1D1中,AA1=1,AB=AD=2,E,F分別是棱AB,BC的中點,證明A1,C1,F,E四點共面,并求點B到平面A1EF的距離.查看答案和解析>>
科目:高中數學 來源: 題型:選擇題

| A. | $\overrightarrow{AD}$與$\overrightarrow{BC}$ | B. | $\overrightarrow{OA}$與$\overrightarrow{OB}$ | C. | $\overrightarrow{AC}$與$\overrightarrow{BD}$ | D. | $\overrightarrow{EO}$與$\overrightarrow{OF}$ |
查看答案和解析>>
科目:高中數學 來源: 題型:解答題
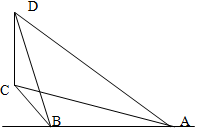 一輛汽車在一條水平的公路上向正西行駛,到A處時測得公路北側遠處一山頂D在西偏北15.的方向上,行駛5km后到達B處,測得此山頂在西偏北45.的方向上,此時看山頂的仰角為30,求此山CD的高.
一輛汽車在一條水平的公路上向正西行駛,到A處時測得公路北側遠處一山頂D在西偏北15.的方向上,行駛5km后到達B處,測得此山頂在西偏北45.的方向上,此時看山頂的仰角為30,求此山CD的高.查看答案和解析>>
科目:高中數學 來源: 題型:解答題
查看答案和解析>>
科目:高中數學 來源: 題型:解答題
查看答案和解析>>
科目:高中數學 來源: 題型:解答題
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com