
分析 以$\frac{π}{4}$分界點進行討論,確定函數的單調性,利用函數的圖形,畫出草圖進行求解,即可得到結果
解答 解:∵當x∈[0,$\frac{π}{2}$]時,0<f(x)<1,f(x)為偶函數,
當x∈(0,$\frac{π}{2}$)且x≠$\frac{π}{4}$時,(x-$\frac{π}{4}$)f'(x)<0,
∴x∈[0,$\frac{π}{4}$]時,f(x)為單調增函數;x∈[$\frac{π}{4}$,$\frac{π}{2}$]時,f(x)為單調減函數,
在同一坐標系中作出y=cos2x和y=f(x)草圖象如下,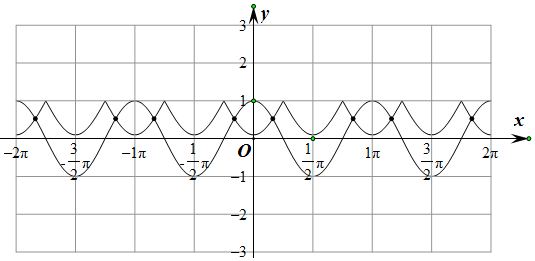
由圖知f(x)=cos2x在[-2π,2π]上的零點個數為8個.
故答案為8.
點評 本題考查函數的單調性,考查函數的零點,考查函數的周期性與奇偶性,利用數形結合的思想來求解,會化難為易.


 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小學生10分鐘應用題系列答案
小學生10分鐘應用題系列答案科目:高中數學 來源: 題型:解答題
查看答案和解析>>
科目:高中數學 來源: 題型:解答題
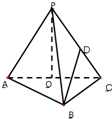 如圖,在三棱錐P-ABC中,AB⊥BC,AB=BC=PA=a,點O、D分別是AC、PC的中點,OP⊥底面ABC.
如圖,在三棱錐P-ABC中,AB⊥BC,AB=BC=PA=a,點O、D分別是AC、PC的中點,OP⊥底面ABC.查看答案和解析>>
科目:高中數學 來源: 題型:解答題
查看答案和解析>>
科目:高中數學 來源: 題型:選擇題
| A. | $\frac{\sqrt{13}-1}{2}$ | B. | $\frac{1+\sqrt{13}}{2}$ | C. | $\frac{\sqrt{13}}{2}$ | D. | $\frac{\sqrt{14}}{2}$ |
查看答案和解析>>
科目:高中數學 來源: 題型:解答題
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com