
分析 (1)通過對f(x)=x3+ax2+bx+1求導可知g(x)=f′(x)=3x2+2ax+b,進而再求導可知g′(x)=6x+2a,通過令g′(x)=0進而可知f′(x)的極小值點為x=-$\frac{a}{3}$,從而f(-$\frac{a}{3}$)=0,整理可知b=$\frac{2{a}^{2}}{9}$+$\frac{3}{a}$(a>0),結合f(x)=x3+ax2+bx+1(a>0,b∈R)有極值可知f′(x)=0有兩個不等的實根,進而可知a>3.
(2)通過(1)構造函數h(a)=b2-3a=$\frac{4{a}^{4}}{81}$-$\frac{5a}{3}$+$\frac{9}{{a}^{2}}$=$\frac{1}{81{a}^{2}}$(4a3-27)(a3-27),結合a>3可知h(a)>0,從而可得結論;
(3)通過(1)可知f′(x)的極小值為f′(-$\frac{a}{3}$)=b-$\frac{{a}^{2}}{3}$,利用韋達定理及完全平方關系可知y=f(x)的兩個極值之和為$\frac{4{a}^{3}}{27}$-$\frac{2ab}{3}$+2,進而問題轉化為解不等式b-$\frac{{a}^{2}}{3}$+$\frac{4{a}^{3}}{27}$-$\frac{2ab}{3}$+2=$\frac{3}{a}$-$\frac{{a}^{2}}{9}$≥-$\frac{7}{2}$,因式分解即得結論.
解答 (1)解:因為f(x)=x3+ax2+bx+1,
所以g(x)=f′(x)=3x2+2ax+b,g′(x)=6x+2a,
令g′(x)=0,解得x=-$\frac{a}{3}$.
由于當x>-$\frac{a}{3}$時g′(x)>0,g(x)=f′(x)單調遞增;當x<-$\frac{a}{3}$時g′(x)<0,g(x)=f′(x)單調遞減;
所以f′(x)的極小值點為x=-$\frac{a}{3}$,
由于導函數f′(x)的極值點是原函數f(x)的零點,
所以f(-$\frac{a}{3}$)=0,即-$\frac{{a}^{3}}{27}$+$\frac{{a}^{3}}{9}$-$\frac{ab}{3}$+1=0,
所以b=$\frac{2{a}^{2}}{9}$+$\frac{3}{a}$(a>0).
因為f(x)=x3+ax2+bx+1(a>0,b∈R)有極值,
所以f′(x)=3x2+2ax+b=0的實根,
所以4a2-12b≥0,即a2-$\frac{2{a}^{2}}{3}$+$\frac{9}{a}$≥0,解得a≥3,
所以b=$\frac{2{a}^{2}}{9}$+$\frac{3}{a}$(a≥3).
(2)證明:由(1)可知h(a)=b2-3a=$\frac{4{a}^{4}}{81}$-$\frac{5a}{3}$+$\frac{9}{{a}^{2}}$=$\frac{1}{81{a}^{2}}$(4a3-27)(a3-27),
由于a>3,所以h(a)>0,即b2>3a;
(3)解:由(1)可知f′(x)的極小值為f′(-$\frac{a}{3}$)=b-$\frac{{a}^{2}}{3}$,
設x1,x2是y=f(x)的兩個極值點,則x1+x2=$-\frac{2a}{3}$,x1x2=$\frac{b}{3}$,
所以f(x1)+f(x2)=${{x}_{1}}^{3}$+${{x}_{2}}^{3}$+a(${{x}_{1}}^{2}$+${{x}_{2}}^{2}$)+b(x1+x2)+2
=(x1+x2)[(x1+x2)2-3x1x2]+a[(x1+x2)2-2x1x2]+b(x1+x2)+2
=$\frac{4{a}^{3}}{27}$-$\frac{2ab}{3}$+2,
又因為f(x),f′(x)這兩個函數的所有極值之和不小于-$\frac{7}{2}$,
所以b-$\frac{{a}^{2}}{3}$+$\frac{4{a}^{3}}{27}$-$\frac{2ab}{3}$+2=$\frac{3}{a}$-$\frac{{a}^{2}}{9}$≥-$\frac{7}{2}$,
因為a>3,所以2a3-63a-54≤0,
所以2a(a2-36)+9(a-6)≤0,
所以(a-6)(2a2+12a+9)≤0,
由于a>3時2a2+12a+9>0,
所以a-6≤0,解得a≤6,
所以a的取值范圍是(3,6].
點評 本題考查利用導數研究函數的單調性、極值,考查運算求解能力,考查轉化思想,注意解題方法的積累,屬于難題.


 考前必練系列答案
考前必練系列答案科目:高中數學 來源: 題型:填空題
查看答案和解析>>
科目:高中數學 來源: 題型:解答題
 如圖,在三棱錐A-BCD中,AB⊥AD,BC⊥BD,平面ABD⊥平面BCD,點E、F(E與A、D不重合)分別在棱AD,BD上,且EF⊥AD.
如圖,在三棱錐A-BCD中,AB⊥AD,BC⊥BD,平面ABD⊥平面BCD,點E、F(E與A、D不重合)分別在棱AD,BD上,且EF⊥AD.查看答案和解析>>
科目:高中數學 來源: 題型:填空題
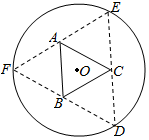 如圖,圓形紙片的圓心為O,半徑為5cm,該紙片上的等邊三角形ABC的中心為O.D、E、F為圓O上的點,△DBC,△ECA,△FAB分別是以BC,CA,AB為底邊的等腰三角形.沿虛線剪開后,分別以BC,CA,AB為折痕折起△DBC,△ECA,△FAB,使得D、E、F重合,得到三棱錐.當△ABC的邊長變化時,所得三棱錐體積(單位:cm3)的最大值為4$\sqrt{15}$cm3.
如圖,圓形紙片的圓心為O,半徑為5cm,該紙片上的等邊三角形ABC的中心為O.D、E、F為圓O上的點,△DBC,△ECA,△FAB分別是以BC,CA,AB為底邊的等腰三角形.沿虛線剪開后,分別以BC,CA,AB為折痕折起△DBC,△ECA,△FAB,使得D、E、F重合,得到三棱錐.當△ABC的邊長變化時,所得三棱錐體積(單位:cm3)的最大值為4$\sqrt{15}$cm3.查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com