
分析 根據分段函數的表達式,分別討論x的取值范圍,進行求解即可.
解答 解:若x≤0,則x-$\frac{1}{2}$≤-$\frac{1}{2}$,
則f(x)+f(x-$\frac{1}{2}$)>1等價為x+1+x-$\frac{1}{2}$+1>1,即2x>-$\frac{1}{2}$,則x>$-\frac{1}{4}$,
此時$-\frac{1}{4}$<x≤0,
當x>0時,f(x)=2x>1,x-$\frac{1}{2}$>-$\frac{1}{2}$,
當x-$\frac{1}{2}$>0即x>$\frac{1}{2}$時,滿足f(x)+f(x-$\frac{1}{2}$)>1恒成立,
當0≥x-$\frac{1}{2}$>-$\frac{1}{2}$,即$\frac{1}{2}$≥x>0時,f(x-$\frac{1}{2}$)=x-$\frac{1}{2}$+1=x+$\frac{1}{2}$$>\frac{1}{2}$,
此時f(x)+f(x-$\frac{1}{2}$)>1恒成立,
綜上x>$-\frac{1}{4}$,
故答案為:($-\frac{1}{4}$,+∞).
點評 本題主要考查不等式的求解,結合分段函數的不等式,利用分類討論的數學思想進行求解是解決本題的關鍵.


科目:高中數學 來源: 題型:選擇題
| A. | {x|-2<x<-1} | B. | {x|-2<x<3} | C. | {x|-1<x<1} | D. | {x|1<x<3} |
查看答案和解析>>
科目:高中數學 來源: 題型:解答題
查看答案和解析>>
科目:高中數學 來源: 題型:解答題
查看答案和解析>>
科目:高中數學 來源: 題型:解答題
查看答案和解析>>
科目:高中數學 來源: 題型:解答題
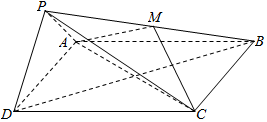 如圖,在四棱錐P-ABCD中,底面ABCD為正方形,平面PAD⊥平面ABCD,點M在線段PB上,PD∥平面MAC,PA=PD=$\sqrt{6}$,AB=4.
如圖,在四棱錐P-ABCD中,底面ABCD為正方形,平面PAD⊥平面ABCD,點M在線段PB上,PD∥平面MAC,PA=PD=$\sqrt{6}$,AB=4.查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com