
分析 (1)由已知利用余弦定理即可解得得解b的值.
(2)利用余弦定理可求cosC的值,結合同角三角函數基本關系式可求sinC的值,進而利用二倍角公式即可計算得解.
解答 解:(1)由余弦定理,b2=a2+c2-2accosB,可得:${b^2}={2^2}+{3^2}-2×2×3×\frac{1}{4}=10$,
∴解得:$b=\sqrt{10}$.
(2)∵$cosC=\frac{{{a^2}+{b^2}-{c^2}}}{2ab}$=$\frac{4+10-9}{{2×2×\sqrt{10}}}=\frac{{\sqrt{10}}}{8}$,
又∵C是△ABC的內角,
∴$sinC=\frac{{3\sqrt{6}}}{8}$.
∴sin2C=2sinCcosC=2×$\frac{3\sqrt{6}}{8}$×$\frac{\sqrt{10}}{8}$=$\frac{3\sqrt{15}}{16}$.
點評 本題主要考查了余弦定理,同角三角函數基本關系式,二倍角公式在解三角形中的應用,考查了計算能力和轉化思想,屬于基礎題.


科目:高中數學 來源: 題型:解答題
查看答案和解析>>
科目:高中數學 來源: 題型:選擇題
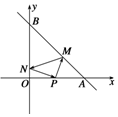 如圖,已知A(4,0)、B(0,4),從點P(2,0),點M是線段AB上一點,點N是y軸上一點,則|PM|+|PN|+|MN|的最小值是 ( )
如圖,已知A(4,0)、B(0,4),從點P(2,0),點M是線段AB上一點,點N是y軸上一點,則|PM|+|PN|+|MN|的最小值是 ( )| A. | 2$\sqrt{10}$ | B. | 6 | C. | 3$\sqrt{3}$ | D. | 2$\sqrt{5}$ |
查看答案和解析>>
科目:高中數學 來源: 題型:填空題
查看答案和解析>>
科目:高中數學 來源: 題型:填空題
查看答案和解析>>
科目:高中數學 來源: 題型:解答題
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com