
分析 (1)根據(jù)獎(jiǎng)勵(lì)方案,可得分段函數(shù);
(2)確定x>15,利用函數(shù)解析式,即可得到結(jié)論.
解答 解:(1)由題意,當(dāng)銷售利潤(rùn)不超過(guò)8萬(wàn)元時(shí),按銷售利潤(rùn)的1%進(jìn)行獎(jiǎng)勵(lì);當(dāng)銷售利潤(rùn)超過(guò)8萬(wàn)元時(shí),若超出A萬(wàn)元,則超出部分按log5(2A+1)進(jìn)行獎(jiǎng)勵(lì),
∴0<x≤8時(shí),y=0.15x;x>8時(shí),y=1.2+log5(2x-15)
∴獎(jiǎng)金y關(guān)于銷售利潤(rùn)x的關(guān)系式y(tǒng)=$\left\{\begin{array}{l}{0.15x,0≤x≤8}\\{1.2+lo{g}_{5}(2x-15),x>8}\end{array}\right.$
(2)由題意知1.2+log5(2x-15)=3.2,解得x=20.
所以,小江的銷售利潤(rùn)是20萬(wàn)元.
點(diǎn)評(píng) 本題以實(shí)際問(wèn)題為載體,考查函數(shù)模型的構(gòu)建,考查學(xué)生的計(jì)算能力,屬于中檔題.



| 年級(jí) | 高中課程 | 年級(jí) | 初中課程 |
| 高一 | 高一免費(fèi)課程推薦! | 初一 | 初一免費(fèi)課程推薦! |
| 高二 | 高二免費(fèi)課程推薦! | 初二 | 初二免費(fèi)課程推薦! |
| 高三 | 高三免費(fèi)課程推薦! | 初三 | 初三免費(fèi)課程推薦! |
科目:高中數(shù)學(xué) 來(lái)源: 題型:選擇題
| A. | x≥0 | B. | x<0或x>2 | C. | x<-$\frac{1}{2}$ | D. | x≤-$\frac{1}{2}$或x≥3 |
查看答案和解析>>
科目:高中數(shù)學(xué) 來(lái)源: 題型:選擇題

| A. | k>98? | B. | k≥99? | C. | k≥100? | D. | k>101? |
查看答案和解析>>
科目:高中數(shù)學(xué) 來(lái)源: 題型:解答題
查看答案和解析>>
科目:高中數(shù)學(xué) 來(lái)源: 題型:選擇題
| A. | (1,3) | B. | (1,2) | C. | [2,3) | D. | (1,2] |
查看答案和解析>>
科目:高中數(shù)學(xué) 來(lái)源: 題型:選擇題
| A. | 8 | B. | -8 | C. | 11 | D. | -11 |
查看答案和解析>>
科目:高中數(shù)學(xué) 來(lái)源: 題型:選擇題
| A. | $(\frac{2}{{3{e^2}}},\frac{1}{2e})$ | B. | $(\frac{2}{{3{e^2}}},\frac{1}{e})$ | C. | $[\frac{2}{{3{e^2}}},\frac{1}{2e})$ | D. | $[\frac{2}{{3{e^2}}},\frac{1}{e})$ |
查看答案和解析>>
科目:高中數(shù)學(xué) 來(lái)源: 題型:填空題
查看答案和解析>>
科目:高中數(shù)學(xué) 來(lái)源: 題型:解答題
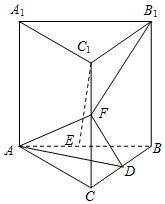 如圖,在直三棱柱ABC-A1B1C1中,AB=AC=AA1=3,D、E分別是BC、AB的中點(diǎn),F(xiàn)是CC1上一點(diǎn),且CF=2C1F.
如圖,在直三棱柱ABC-A1B1C1中,AB=AC=AA1=3,D、E分別是BC、AB的中點(diǎn),F(xiàn)是CC1上一點(diǎn),且CF=2C1F.查看答案和解析>>
百度致信 - 練習(xí)冊(cè)列表 - 試題列表
湖北省互聯(lián)網(wǎng)違法和不良信息舉報(bào)平臺(tái) | 網(wǎng)上有害信息舉報(bào)專區(qū) | 電信詐騙舉報(bào)專區(qū) | 涉歷史虛無(wú)主義有害信息舉報(bào)專區(qū) | 涉企侵權(quán)舉報(bào)專區(qū)
違法和不良信息舉報(bào)電話:027-86699610 舉報(bào)郵箱:58377363@163.com