
設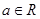 ,函數
,函數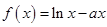 .
.
(1)若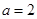 ,求曲線
,求曲線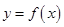 在點
在點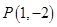 處的切線方程;
處的切線方程;
(2)若 無零點,求實數
無零點,求實數 的取值范圍;
的取值范圍;
(3)若 有兩個相異零點
有兩個相異零點 、
、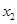 ,求證:
,求證: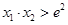 .
.
(1)切線方程為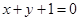 ;(2)實數
;(2)實數 的取值范圍是
的取值范圍是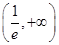 ;(3)詳見解析.
;(3)詳見解析.
解析試題分析:(1)將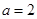 代入函數
代入函數 的解析式,利用導函數的幾何意義,結合直線的點斜式求出切線的方程;(2)先求出函數
的解析式,利用導函數的幾何意義,結合直線的點斜式求出切線的方程;(2)先求出函數 的導數,對
的導數,對 的符號進行分類討論,結合零點存在定理判斷函數
的符號進行分類討論,結合零點存在定理判斷函數 在定義域上是否有零點,從而求出參數
在定義域上是否有零點,從而求出參數 的取值范圍;另外一中方法是將問題等價轉化為“直線
的取值范圍;另外一中方法是將問題等價轉化為“直線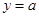 與曲線
與曲線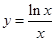 無公共點”,結合導數研究函數
無公共點”,結合導數研究函數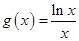 的基本性質,然后利用圖象即可確定實數
的基本性質,然后利用圖象即可確定實數 的取值范圍;(3)從所證的不等式出發,利用分析法最終將問題等價轉換為證明不等式
的取值范圍;(3)從所證的不等式出發,利用分析法最終將問題等價轉換為證明不等式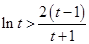 在區間
在區間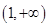 上恒成立,并構造新函數
上恒成立,并構造新函數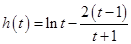 ,利用導數結合函數的單調性與最值來進行證明.
,利用導數結合函數的單調性與最值來進行證明.
試題解析:在區間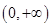 上,
上,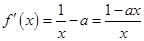 ,
,
(1)當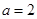 時,
時,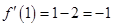 ,則切線方程為
,則切線方程為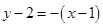 ,即
,即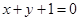 ;
;
(2)①當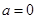 時,
時,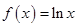 有唯一零點
有唯一零點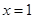 ;
;
②當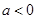 時,則
時,則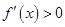 ,
, 是區間
是區間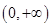 上的增函數,
上的增函數,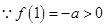 ,
, ,
,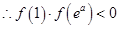 ,即函數
,即函數 在區間
在區間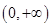 有唯一零點;
有唯一零點;
③當 時,令
時,令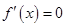 得
得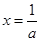 ,
,
在區間 上,
上,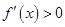 ,函數
,函數 是增函數,
是增函數,
在區間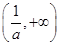 上,
上,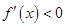 ,函數
,函數 是減函數,
是減函數,
故在區間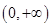 上,
上, 的極大值為
的極大值為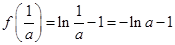 ,
,
由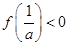 ,即
,即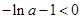 ,解得
,解得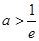 ,故所求實數
,故所求實數 的取值范圍是
的取值范圍是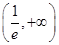 ;
;
另解: 無零點
無零點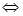 方程
方程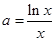 在
在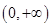 上無實根
上無實根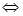 直線
直線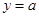 與曲線
與曲線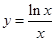 無公共點,
無公共點,
令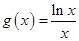 ,則
,則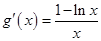 ,令
,令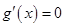 ,解得
,解得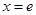 ,列表如下:
,列表如下: