
已知函數
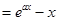 ,其中
,其中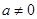 .
.
(1)若對一切x∈R, ≥1恒成立,求a的取值集合;
≥1恒成立,求a的取值集合;
(2)在函數 的圖像上取定兩點
的圖像上取定兩點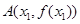 ,
,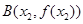
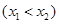 ,記直線AB的斜率 為k,問:是否存在x0∈(x1,x2),使
,記直線AB的斜率 為k,問:是否存在x0∈(x1,x2),使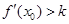 成立?若存在,求
成立?若存在,求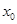 的取值范圍;若不存在,請說明理由.
的取值范圍;若不存在,請說明理由.
(1)  的取值集合為
的取值集合為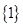 ;
;
(2)存在 使
使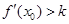 成立.且
成立.且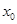 的取值范圍為
的取值范圍為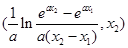
解析試題分析:(1)利用導數求出 的最小值,令其大于等于
的最小值,令其大于等于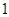 即
即 ,解得
,解得 的取值集合; (2)由題意知
的取值集合; (2)由題意知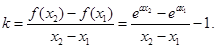 ,令
,令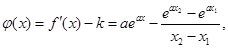 然后說明在
然后說明在 內
內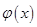 有唯一零點
有唯一零點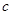 且
且 ,故當且僅當
,故當且僅當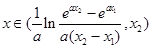 時,
時, 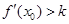 .
.
試題解析:(1)若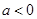 ,則對一切
,則對一切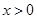 ,
,
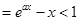 ,
,
這與題設矛盾,又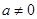 ,故
,故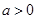 .
.
而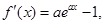 令
令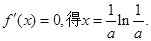
當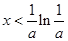 時,
時, 單調遞減;當
單調遞減;當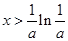 時,
時,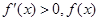 單調遞增,故當
單調遞增,故當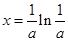 時,
時,  取最小值
取最小值
于是對一切 恒成立,當且僅當
恒成立,當且僅當 . ①
. ①
令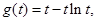 則
則
當 時,
時,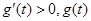 單調遞增;當
單調遞增;當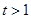 時,
時,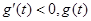 單調遞減.
單調遞減.
故當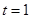 時,
時,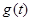 取最大值
取最大值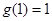 .因此,當且僅當
.因此,當且僅當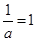 即
即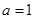 時,①式成立.
時,①式成立.
綜上所述, 的取值集合為
的取值集合為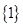 .
.
(2)由題意知,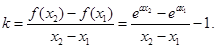
令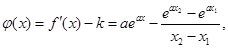 則
則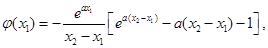
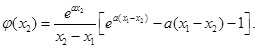
令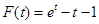 ,則
,則 .
.
當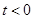 時,
時, 單調遞減;當
單調遞減;當 時,
時,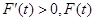 單調遞增.
單調遞增.
故當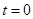 ,
,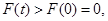 即
即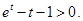
從而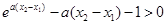 ,
,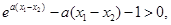 又
又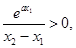
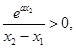
所以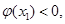
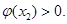
因為函數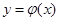 在區間
在區間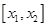 上的圖像是連續不斷的一條曲線,所以存在
上的圖像是連續不斷的一條曲線,所以存在 使
使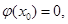
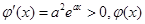 單調遞增,故這樣的
單調遞增,故這樣的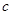 是唯一的,且
是唯一的,且 .故當且僅當
.故當且僅當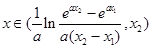 時,
時, 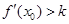 .
.
綜上所述,存在 使
使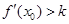 成立.且
成立.且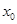 的取值范圍為
的取值范圍為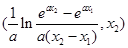 .
.
考點:直線斜率定義、利用導數求函數最值、利用導數求函數單調性、零點存在定理.


 鷹派教輔銜接教材河北教育出版社系列答案
鷹派教輔銜接教材河北教育出版社系列答案 初中暑期銜接系列答案
初中暑期銜接系列答案科目:高中數學 來源: 題型:解答題
某校內有一塊以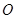 為圓心,
為圓心,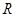 (
(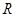 為常數,單位為米)為半徑的半圓形(如圖)荒地,該校總務處計劃對其開發利用,其中弓形
為常數,單位為米)為半徑的半圓形(如圖)荒地,該校總務處計劃對其開發利用,其中弓形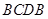 區域(陰影部分)用于種植學校觀賞植物,
區域(陰影部分)用于種植學校觀賞植物,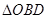 區域用于種植花卉出售,其余區域用于種植草皮出售.已知種植學校觀賞植物的成本是每平方米20元,種植花卉的利潤是每平方米80元,種植草皮的利潤是每平方米30元.
區域用于種植花卉出售,其余區域用于種植草皮出售.已知種植學校觀賞植物的成本是每平方米20元,種植花卉的利潤是每平方米80元,種植草皮的利潤是每平方米30元.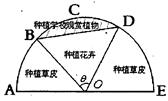
(1)設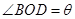 (單位:弧度),用
(單位:弧度),用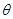 表示弓形
表示弓形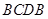 的面積
的面積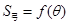 ;
;
(2)如果該校總務處邀請你規劃這塊土地,如何設計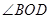 的大小才能使總利潤最大?并求出該最大值.
的大小才能使總利潤最大?并求出該最大值.
(參考公式:扇形面積公式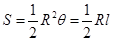 ,
,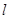 表示扇形的弧長)
表示扇形的弧長)
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com