
已知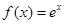 ,
,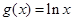 .
.
(Ⅰ)求證: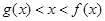 ;
;
(Ⅱ)設直線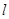 與
與 、
、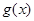 均相切,切點分別為(
均相切,切點分別為(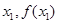 )、(
)、(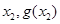 ),且
),且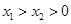 ,求證:
,求證: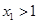 .
.
(Ⅰ) 見解析;(Ⅱ)見解析.
解析試題分析:(Ⅰ)先構造函數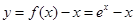 ,利用函數的單調性與導數的關系,求得函數的最小值是
,利用函數的單調性與導數的關系,求得函數的最小值是 ,找到關系
,找到關系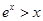 ;再構造函數
;再構造函數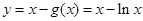 ,利用函數的單調性與導數的關系,求得函數的最小值是
,利用函數的單調性與導數的關系,求得函數的最小值是 ,找到關系
,找到關系 .從而證得“
.從而證得“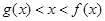 ”;(Ⅲ)先求出
”;(Ⅲ)先求出 以及
以及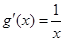 ,根據導數與切線方程的關系,由斜率不變得到
,根據導數與切線方程的關系,由斜率不變得到 ,再根據兩點間的斜率公式得到
,再根據兩點間的斜率公式得到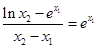 .首先由指數函數的性質可得
.首先由指數函數的性質可得 ,那么
,那么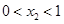 ,然后由
,然后由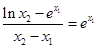 得到
得到 ,解得
,解得 .
.
試題解析:(Ⅰ)令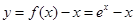 ,
, . 1分
. 1分
令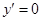 ,解得
,解得 .
.
當 時,
時,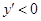 ;當
;當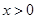 ,時
,時 .
.
∴當 時,
時, ,
,
∴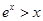 . 3分
. 3分
令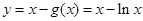 ,
,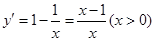 . 4分
. 4分
令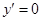 ,解得
,解得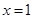 .
.
當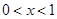 時,
時,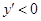 ;當
;當 時,
時, .
.
∴當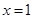 時,
時, ,
,
∴ , 6分
, 6分
∴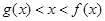 . 7分
. 7分
(Ⅲ) ,
,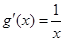 ,切點的坐標分別為
,切點的坐標分別為 ,可得方程組:
,可得方程組: 11分
11分
∵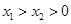 ,
,
∴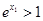 ,∴
,∴ ,
,
∴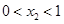 . 12分
. 12分
由②得,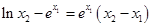 ,∴
,∴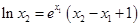 , 13分
, 13分
∵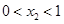 ,∴
,∴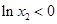 ,∴
,∴ ,即
,即 ,
,
∴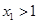 . 14分
. 14分
考點:1.分類討論思想;2.函數的單調性與導數的關系;3.對數函數的性質;4.指數函數的性質;5.利用導數研究曲線的切線方程


 口算小狀元口算速算天天練系列答案
口算小狀元口算速算天天練系列答案 天天練口算系列答案
天天練口算系列答案科目:高中數學 來源: 題型:解答題
設a為實數,函數f(x)=ex-2x+2a,x∈R.
(Ⅰ)求f(x)的單調區間與極值;
(Ⅱ)求證:當a>ln2-1且x>0時,ex>x2-2ax+1.
查看答案和解析>>
科目:高中數學 來源: 題型:解答題
如圖,某自來水公司要在公路兩側鋪設水管,公路為東西方向,在路北側沿直線鋪設線路l1,在路南側沿直線鋪設線路l2,現要在矩形區域ABCD內沿直線將l1與l2接通.已知AB = 60m,BC = 80m,公路兩側鋪設水管的費用為每米1萬元,穿過公路的EF部分鋪設水管的費用為每米2萬元,設∠EFB= α,矩形區域內的鋪設水管的總費用為W.
(1)求W關于α的函數關系式;
(2)求W的最小值及相應的角α.
查看答案和解析>>
科目:高中數學 來源: 題型:解答題
某出版社新出版一本高考復習用書,該書的成本為5元/本,經銷過程中每本書需付給代理商m元(1≤m≤3)的勞務費,經出版社研究決定,新書投放市場后定價為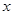 元/本(9≤
元/本(9≤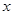 ≤11),預計一年的銷售量為
≤11),預計一年的銷售量為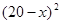 萬本.
萬本.
(1)求該出版社一年的利潤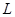 (萬元)與每本書的定價
(萬元)與每本書的定價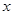 的函數關系式;
的函數關系式;
(2)當每本書的定價為多少元時,該出版社一年的利潤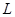 最大,并求出
最大,并求出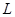 的最大值
的最大值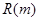 .
.
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com