
| A. | $\frac{1}{4}$ | B. | $\frac{1}{3}$ | C. | $\frac{1}{2}$ | D. | $\frac{2}{3}$ |
分析 根據已知中A是圓上固定的一定點,在圓上其他位置任取一點B,連接A、B兩點,它是一條弦,我們求出B點位置所有基本事件對應的弧長,及滿足條件AB長大于半徑的基本事件對應的弧長,代入幾何概型概率計算公式,即可得到答案
解答 解:在圓上其他位置任取一點N,設圓半徑為R,
則N點位置所有情況對應的弧長為圓的周長2πR,
其中滿足條件MN的長度不小于半徑長度的對應的弧長為 $\frac{2}{3}$•2πR,
則AB弦的長度大于等于半徑長度的概率P=$\frac{\frac{2}{3}•2πR}{2πR}=\frac{2}{3}$;
故選D.
點評 本題考查的知識點是幾何概型,其中根據已知條件計算出所有基本事件對應的幾何量及滿足條件的基本事件對應的幾何量是解答的關鍵.


科目:高中數學 來源: 題型:選擇題
| A. | -1 | B. | 0 | C. | 1 | D. | 2 |
查看答案和解析>>
科目:高中數學 來源: 題型:解答題
查看答案和解析>>
科目:高中數學 來源: 題型:選擇題
| A. | 數列{An}是等差數列,數列{Bn}是等比數列 | |
| B. | 數列{An}與{Bn}都是等差數列 | |
| C. | 數列{An}是等比數列,數列{Bn}是等差數列 | |
| D. | 數列{An}與{Bn}都是等比數列 |
查看答案和解析>>
科目:高中數學 來源: 題型:選擇題
| A. | θ=$\frac{π}{12}$,t的最小值為$\frac{π}{12}$ | B. | θ=$\frac{π}{12}$,t的最小值為$\frac{π}{6}$ | ||
| C. | θ=$\frac{π}{6}$,t的最小值為$\frac{π}{6}$ | D. | θ=$\frac{π}{6}$,t的最小值為$\frac{π}{12}$ |
查看答案和解析>>
科目:高中數學 來源: 題型:選擇題
| A. | 0 | B. | 1 | C. | 2 | D. | 3 |
查看答案和解析>>
科目:高中數學 來源: 題型:選擇題
| A. | $\frac{1}{2}$ | B. | $\frac{1}{3}$ | C. | $\frac{1}{4}$ | D. | $\frac{1}{5}$ |
查看答案和解析>>
科目:高中數學 來源: 題型:解答題
查看答案和解析>>
科目:高中數學 來源: 題型:解答題
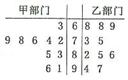 渝州集團對所有員工進行了職業技能測試從甲、乙兩部門中各任選10名員工的測試成績(單位:分)數據的莖葉圖如圖所示.
渝州集團對所有員工進行了職業技能測試從甲、乙兩部門中各任選10名員工的測試成績(單位:分)數據的莖葉圖如圖所示.| 分數 | [60,70) | [70,80) | [80,90) | [90,100] |
| 獎金 | a | 2a | 3a | 4a |
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com