
分析 (1)求出原函數的導函數,求得導函數的零點,然后對a分類求出函數的單調區間.
(2)由(1)可知,f(x)在(3,4]上單調遞增.求出f(x)在(3,4]上的最大值,把問題轉化為f(x)max+lna+1>$m(a-{a}^{2})+2aln\frac{4}{e}$,即2-2a+lna>m(a-a2)恒成立.即對任意的a∈(1,$\sqrt{2}$),不等式lna+ma2-(m+2)a+2>0恒成立.設h(a)=lna+ma2-(m+2)a+2,然后分m≥1和m<1討論a∈(1,$\sqrt{2}$)時h(a)>0是否恒成立求得實數m的取值范圍.
解答 解:(1)f′(x)=$\frac{2a}{x}+2x-(a+4)=\frac{(x-2)(2x-a)}{x}$.
令f′(x)=0,得x1=2,${x}_{2}=\frac{a}{2}$.
①當a>4時,$\frac{a}{2}$>2,當2<x<$\frac{a}{2}$時,f′(x)<0;當0<x<2時,f′(x)>0.
此時f(x)的單調增區間為(0,2),($\frac{a}{2},+∞$),單調遞減區間為(2,$\frac{a}{2}$).
②當a=4時,$\frac{a}{2}$=2,f′(x)=$\frac{2(x-2)^{2}}{x}≥$0,f(x)在(0,+∞)上單調遞增.
③當0<a<4時,$\frac{a}{2}$<2,當$\frac{a}{2}$<x<2時,f′(x)<0;當0<x<$\frac{a}{2}$或x>2時,f′(x)>0.
此時f(x)的單調增區間為(0,$\frac{a}{2}$),(2,+∞),單調遞減區間為($\frac{a}{2}$,2).
綜上所述,當a>4時,f(x)的單調增區間為(0,2),($\frac{a}{2},+∞$),單調遞減區間為(2,$\frac{a}{2}$).
當a=4時,f(x)在(0,+∞)上單調遞增.
當0<a<4時,f(x)的單調增區間為(0,$\frac{a}{2}$),(2,+∞),單調遞減區間為($\frac{a}{2}$,2).
(2)由(1)可知,當a∈(1,$\sqrt{2}$)時,f(x)在(3,4]上單調遞增.
∴x∈(3,4]時,f(x)max=f(4)=4aln2-4a+1,依題意,
只需f(x)max+lna+1>$m(a-{a}^{2})+2aln\frac{4}{e}$,即2-2a+lna>m(a-a2)恒成立.
即對任意的a∈(1,$\sqrt{2}$),不等式lna+ma2-(m+2)a+2>0恒成立.
設h(a)=lna+ma2-(m+2)a+2,則h(1)=0.
$h′(a)=\frac{1}{a}+2ma-(m+2)=\frac{(2a-1)(ma-1)}{a}$.
∵a∈(1,$\sqrt{2}$),∴$\frac{2a-1}{a}$>0.
①當m≥1時,對任意的a∈(1,$\sqrt{2}$),ma-1>0,∴h′(a)>0,h(a)在(1,$\sqrt{2}$)上單調遞增,h(a)>h(1)=0恒成立;
②當m<1時,存在a0∈(1,$\sqrt{2}$),使得當a∈(1,a0)時,ma-1<0,∴h′(a)<0,h(a)單調遞減,h(a)<h(1)=0,
∴a∈(1,$\sqrt{2}$)時,h(a)>0不能恒成立.
綜上述,實數m的取值范圍是[1,+∞).
點評 本題考查利用導數研究函數的單調性,考查了利用導數求函數的最值,考查分類討論的數學思想方法和數學轉化思想方法,是壓軸題.


科目:高中數學 來源: 題型:解答題
查看答案和解析>>
科目:高中數學 來源: 題型:選擇題
| A. | $\frac{1}{4}$ | B. | $\frac{1}{3}$ | C. | $\frac{1}{2}$ | D. | $\frac{2}{3}$ |
查看答案和解析>>
科目:高中數學 來源: 題型:解答題
查看答案和解析>>
科目:高中數學 來源: 題型:選擇題
| A. | f($\frac{π}{6}$)>$\sqrt{2}$f($\frac{π}{4}$) | B. | $\sqrt{2}$sin1•f(1)>f($\frac{π}{4}$) | C. | f($\frac{π}{6}$)>$\sqrt{3}$f($\frac{π}{3}$) | D. | $\sqrt{2}$f($\frac{π}{4}$)>$\sqrt{3}$f($\frac{π}{3}$) |
查看答案和解析>>
科目:高中數學 來源: 題型:選擇題
| A. | {0,1,2,4} | B. | {0,1,2} | C. | {1,4} | D. | {0,1,4} |
查看答案和解析>>
科目:高中數學 來源: 題型:選擇題
| A. | 40 | B. | 60 | C. | 80 | D. | 100 |
查看答案和解析>>
科目:高中數學 來源: 題型:解答題
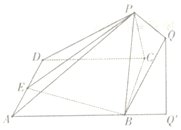 已知如圖所示的幾何體中,四邊形ABCD是邊長為2的菱形,面PBC⊥面A BCD,點E是AD 的中點,PQ∥面ABCD且點Q在面ABCD上的射影Q′落在AB的延長線上,若PQ=1,PB=$\sqrt{2}$,且($\overrightarrow{PB}+\overrightarrow{PC}$)•$\overrightarrow{BC}$=0,$\overrightarrow{AB}•\overrightarrow{AD}$=2
已知如圖所示的幾何體中,四邊形ABCD是邊長為2的菱形,面PBC⊥面A BCD,點E是AD 的中點,PQ∥面ABCD且點Q在面ABCD上的射影Q′落在AB的延長線上,若PQ=1,PB=$\sqrt{2}$,且($\overrightarrow{PB}+\overrightarrow{PC}$)•$\overrightarrow{BC}$=0,$\overrightarrow{AB}•\overrightarrow{AD}$=2查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com