
分析 根據函數奇偶性的性質先求出函數的解析式,進行求解即可.
解答 解:∵函數f(x)是定義在R上的奇函數,
∴f(0)=0,
若x>0,則-x<0,則-x<0,則f(-x)=x2-2=-f(x),
即f(x)=-x2+2,x>0,
當x<0時,不等式f(x)<x等價為x2-2<x,即x2-x-2<0,即-1<x<2,此時-1<x<0,
當x>0時,不等式f(x)<x等價為-x2+2<x,即x2+x-2>0,即x>1或x<-2,此時x>1,
當x=0時,不等式不成立,
綜上不等式的解為-1<x<0或x>1,
即不等式的解集為(1,+∞)∪(-1,0),
故答案為:(1,+∞)∪(-1,0)
點評 本題主要考查不等式的求解,結合函數奇偶性的性質進行轉化求解是解決本題的關鍵.注意要進行分類討論.


科目:高中數學 來源: 題型:填空題
查看答案和解析>>
科目:高中數學 來源: 題型:填空題
查看答案和解析>>
科目:高中數學 來源: 題型:填空題
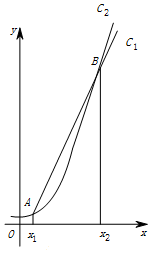 函數f(x)=2x和g(x)=x3的圖象的示意圖如圖所示,設兩函數的圖象交于點A(x1,y1),B(x2,y2),且x1<x2.若x1∈[a,a+1],x2∈[b,b+1],且a,b∈{1,2,3,4,5,6,7,8,9,10,11,12},則a+b=10.
函數f(x)=2x和g(x)=x3的圖象的示意圖如圖所示,設兩函數的圖象交于點A(x1,y1),B(x2,y2),且x1<x2.若x1∈[a,a+1],x2∈[b,b+1],且a,b∈{1,2,3,4,5,6,7,8,9,10,11,12},則a+b=10.查看答案和解析>>
科目:高中數學 來源: 題型:解答題
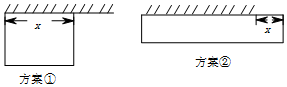 上海市復興高級中學二期改擴建工程于2015年9月正式開始,現需要圍建一個面積火900平方米的矩形地場地的圍墻,有一面長度為20米的舊墻(圖中斜杠部),有甲、乙兩種維修利用舊墻方案.
上海市復興高級中學二期改擴建工程于2015年9月正式開始,現需要圍建一個面積火900平方米的矩形地場地的圍墻,有一面長度為20米的舊墻(圖中斜杠部),有甲、乙兩種維修利用舊墻方案.查看答案和解析>>
科目:高中數學 來源: 題型:選擇題
| A. | f(x1)<f(x2) | B. | f(x1)=f(x2) | ||
| C. | f(x1)>f(x2) | D. | f(x1)、f(x&2)的大小不確定 |
查看答案和解析>>
科目:高中數學 來源: 題型:選擇題
| A. | 奇函數 | B. | 偶函數 | ||
| C. | 既是奇函數又是偶函數 | D. | 非奇非偶函數 |
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com