
 如圖,直三棱柱ABC-A1B1C1中,底面ABC為等腰直角三角形,AB⊥AC,AB=AC=2,AA1=3,M是側(cè)棱CC1上一點(diǎn).
如圖,直三棱柱ABC-A1B1C1中,底面ABC為等腰直角三角形,AB⊥AC,AB=AC=2,AA1=3,M是側(cè)棱CC1上一點(diǎn).分析 (1)以A為坐標(biāo)原點(diǎn),以射線AB、AC、AA1分別為x、y、z軸建立空間直角坐標(biāo)系,求出相關(guān)點(diǎn)的坐標(biāo),$\overrightarrow{BM}=({-2,2,h})$,$\overrightarrow{{A_1}C}=({0,2,-3})$,由BM⊥A1C得$\overrightarrow{BM}•\overrightarrow{{A_1}C}=0$,求出h,然后推出$\frac{{{C_1}M}}{MC}$的值.
(2)求出平面ABM的一個(gè)法向量,利用空間向量數(shù)量積求解直線BA1與平面ABM所成的角為θ的余弦函數(shù)值,即可求解直線BA1與平面ABM所成的角正弦值.
解答 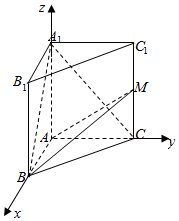 解:(1)以A為坐標(biāo)原點(diǎn),以射線AB、AC、AA1
解:(1)以A為坐標(biāo)原點(diǎn),以射線AB、AC、AA1
分別為x、y、z軸建立空間直角坐標(biāo)系,…(1分)
如圖所示,則B(2,0,0),A1(0,0,3),C(0,2,0),
設(shè)MC=h,則 M(0,2,h)$\overrightarrow{BM}=({-2,2,h})$,$\overrightarrow{{A_1}C}=({0,2,-3})$…(2分)
由BM⊥A1C得$\overrightarrow{BM}•\overrightarrow{{A_1}C}=0$,即2×2-3h=0
解得$h=\frac{4}{3}$,…(5分)
故$\frac{{{C_1}M}}{MC}=\frac{5}{4}$; …(7分)
(2)因?yàn)镸C=2,所以M(0,2,2),$\overrightarrow{AB}=({2,0,0}),\overrightarrow{AM}=({0,2,2}),\overrightarrow{B{A_1}}=({-2,0,3})$
設(shè)平面ABM的一個(gè)法向量為$\vec n=({x,y,z})$,由$\left\{\begin{array}{l}{\vec n•\overrightarrow{AB}=0}\\{\vec n•\overrightarrow{AM}=0}\end{array}$得$\left\{\begin{array}{l}{x=0}\\{y+z=0}\end{array}$,
所以$\vec n=({0,1,-1})$,…(10分)
則cos$<\overrightarrow{n},\overrightarrow{B{A}_{1}}>$=$\frac{\overrightarrow{n}•\overrightarrow{B{A}_{1}}}{|\overrightarrow{n}||\overrightarrow{B{A}_{1}}|}$=$\frac{-3}{\sqrt{2}•\sqrt{13}}$=-$\frac{3\sqrt{26}}{26}$,…(14分)
設(shè)直線BA1與平面ABM所成的角為θ,所以sinθ=|cos$<\overrightarrow{n},\overrightarrow{B{A}_{1}}>$|=$\frac{3\sqrt{26}}{26}$,
所以直線BA1與平面ABM所成的角正弦值為$\frac{{3\sqrt{26}}}{26}$.…(16分).
點(diǎn)評(píng) 本題考查空間向量的數(shù)量積的應(yīng)用,空間向量的垂直,以及線面角的求法,考查空間想象能力以及計(jì)算能力.



| 年級(jí) | 高中課程 | 年級(jí) | 初中課程 |
| 高一 | 高一免費(fèi)課程推薦! | 初一 | 初一免費(fèi)課程推薦! |
| 高二 | 高二免費(fèi)課程推薦! | 初二 | 初二免費(fèi)課程推薦! |
| 高三 | 高三免費(fèi)課程推薦! | 初三 | 初三免費(fèi)課程推薦! |
科目:高中數(shù)學(xué) 來(lái)源: 題型:解答題
 如圖,在△ABC中,D是邊BC上一點(diǎn),$\overrightarrow{BD}=2\overrightarrow{DC},|{\overrightarrow{AD}}$|=1.
如圖,在△ABC中,D是邊BC上一點(diǎn),$\overrightarrow{BD}=2\overrightarrow{DC},|{\overrightarrow{AD}}$|=1.查看答案和解析>>
科目:高中數(shù)學(xué) 來(lái)源: 題型:解答題
查看答案和解析>>
科目:高中數(shù)學(xué) 來(lái)源: 題型:解答題
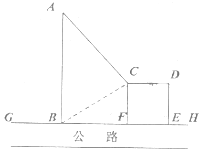 如圖,GH是東西方向的公路北側(cè)的邊緣線,某公司準(zhǔn)備在GH上的一點(diǎn)B的正北方向的A處建設(shè)一倉(cāng)庫(kù),設(shè)AB=ykm,并在公路北側(cè)建造邊長(zhǎng)為xkm的正方形無(wú)頂中轉(zhuǎn)站CDEF(其中EF在GH上),現(xiàn)從倉(cāng)庫(kù)A向GH和中轉(zhuǎn)站分別修兩條道路AB,AC,已知AB=AC+1,且∠ABC=60°..
如圖,GH是東西方向的公路北側(cè)的邊緣線,某公司準(zhǔn)備在GH上的一點(diǎn)B的正北方向的A處建設(shè)一倉(cāng)庫(kù),設(shè)AB=ykm,并在公路北側(cè)建造邊長(zhǎng)為xkm的正方形無(wú)頂中轉(zhuǎn)站CDEF(其中EF在GH上),現(xiàn)從倉(cāng)庫(kù)A向GH和中轉(zhuǎn)站分別修兩條道路AB,AC,已知AB=AC+1,且∠ABC=60°..查看答案和解析>>
科目:高中數(shù)學(xué) 來(lái)源: 題型:填空題
查看答案和解析>>
科目:高中數(shù)學(xué) 來(lái)源: 題型:填空題
查看答案和解析>>
科目:高中數(shù)學(xué) 來(lái)源: 題型:填空題
查看答案和解析>>
百度致信 - 練習(xí)冊(cè)列表 - 試題列表
湖北省互聯(lián)網(wǎng)違法和不良信息舉報(bào)平臺(tái) | 網(wǎng)上有害信息舉報(bào)專(zhuān)區(qū) | 電信詐騙舉報(bào)專(zhuān)區(qū) | 涉歷史虛無(wú)主義有害信息舉報(bào)專(zhuān)區(qū) | 涉企侵權(quán)舉報(bào)專(zhuān)區(qū)
違法和不良信息舉報(bào)電話:027-86699610 舉報(bào)郵箱:58377363@163.com