
| 無促銷活動 | 采用促銷方案1 | 采用促銷方案2 | ||
| 本年度平均銷售額不高于上一年度平均銷售額 | 48 | 11 | 31 | 90 |
| 本年度平均銷售額高于上一年度平均銷售額 | 52 | 69 | 29 | 150 |
| 100 | 80 | 60 |
| 售價x | 33 | 35 | 37 | 39 | 41 | 43 | 45 | 47 |
| 銷量y | 840 | 800 | 740 | 695 | 640 | 580 | 525 | 460 |
| $\hat y=-1200lnx+5000$ | $\hat y=-27x+1700$ | $\hat y=-\frac{1}{3}{x^2}+1200$ | |
| $\sum_{i=1}^8{({y_i}}-{\hat y_i}{)^2}$ | 49428.74 | 11512.43 | 175.26 |
| $\sum_{i=1}^8{({y_i}}-\overline y{)^2}$ | 124650 | ||
分析 (I)根據本年度平均銷售額高于上一年度平均銷售額時,兩種方案的采用數量對比進行選擇;
(II)(i)代入相關指數公式計算即可,并選擇相關指數最大的模型;
(ii)求出利潤關于售價的函數關系式,利用導數求出函數的極大值點即可.
解答 解:(Ⅰ)由列聯表信息可知,年度平均銷售額與方案1的運作相關性強于方案2.
(Ⅱ)(ⅰ)由已知數據可知,回歸模型$\hat y=-1200lnx+5000$對應的相關指數R12=1-$\frac{49428.74}{124650}$=0.6035;
回歸模型$\hat y=-27x+1700$對應的相關指數R22=1-$\frac{11512.43}{124650}$=0.9076;
回歸模型$\hat y=-\frac{1}{3}{x^2}+1200$對應的相關指數R32=1-$\frac{175.26}{124650}$=0.9986.
因為$R_3^2>R_2^2>R_1^2$,所以采用回歸模型$\hat y=-\frac{1}{3}{x^2}+1200$進行擬合最為合適.
(ⅱ)由(Ⅰ)可知,采用方案1的運作效果較方案2好,
故年利潤$z=(-\frac{1}{3}{x^2}+1200)(x-15)$,z'=-(x+30)(x-40),
當x∈(0,40)時,$z=(-\frac{1}{3}{x^2}+1200)(x-15)$單調遞增;
當x∈(40,+∞)時,$z=(-\frac{1}{3}{x^2}+1200)(x-15)$單調遞減.
故當售價x=40時,利潤達到最大.
點評 本題考查了回歸分析,回歸模型的比較,屬于中檔題.


 奪冠訓練單元期末沖刺100分系列答案
奪冠訓練單元期末沖刺100分系列答案 新思維小冠軍100分作業本系列答案
新思維小冠軍100分作業本系列答案 名師指導一卷通系列答案
名師指導一卷通系列答案科目:高中數學 來源: 題型:解答題
查看答案和解析>>
科目:高中數學 來源: 題型:解答題
查看答案和解析>>
科目:高中數學 來源: 題型:填空題
查看答案和解析>>
科目:高中數學 來源: 題型:選擇題
| A. | $\overrightarrow{a}$∥$\overrightarrow{b}$ | B. | $\overrightarrow{a}$⊥$\overrightarrow{b}$ | C. | $\overrightarrow{a}$∥$\overrightarrow{c}$或$\overrightarrow{b}$∥$\overrightarrow{c}$ | D. | $\overrightarrow{a}$⊥$\overrightarrow{c}$或$\overrightarrow{b}$⊥$\overrightarrow{c}$ |
查看答案和解析>>
科目:高中數學 來源: 題型:解答題
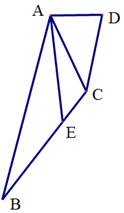 在四邊形ABCD中,點E在BC上,∠BAD=$\frac{2π}{3}$,AD:AC:CD=1:2:$\sqrt{3}$.
在四邊形ABCD中,點E在BC上,∠BAD=$\frac{2π}{3}$,AD:AC:CD=1:2:$\sqrt{3}$.查看答案和解析>>
科目:高中數學 來源: 題型:選擇題
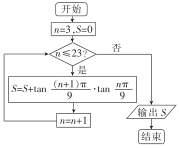
| A. | $-\frac{{2\sqrt{3}}}{{tan\frac{π}{9}}}-21$ | B. | $\frac{{tan\frac{25π}{9}-\sqrt{3}}}{{tan\frac{π}{9}}}-22$ | ||
| C. | $-\frac{{2\sqrt{3}}}{{tan\frac{π}{9}}}-22$ | D. | $\frac{{tan\frac{25π}{9}-\sqrt{3}}}{{tan\frac{π}{9}}}-21$ |
查看答案和解析>>
科目:高中數學 來源: 題型:解答題
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com