
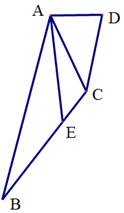
 在四邊形ABCD中,點E在BC上,∠BAD=$\frac{2π}{3}$,AD:AC:CD=1:2:$\sqrt{3}$.
在四邊形ABCD中,點E在BC上,∠BAD=$\frac{2π}{3}$,AD:AC:CD=1:2:$\sqrt{3}$.分析 (1)設AD=k,則AC=2k,CD=$\sqrt{3}k$,利用余弦定理求出$∠CAD=\frac{π}{3}$,由此能求出∠BAC.
(2)設∠AEB=β,EC=m,則∠AEC=π-β,BE=3m,利用正弦定理求出AC=$\frac{1}{3}$,由此利用余弦定理能求出AE.
解答 解:(1)設AD=k,則AC=2k,CD=$\sqrt{3}k$,
在△ACD中,cos∠CAD=$\frac{{k}^{2}+(2k)^{2}-(\sqrt{3}k)^{2}}{2•k•2k}$=$\frac{1}{2}$,
∵∠CAD∈(0,π),∴$∠CAD=\frac{π}{3}$,
∴∠BAC=$∠BAD-∠CAD=\frac{π}{3}$.
(2)設∠AEB=β,EC=m,
則∠AEC=π-β,BE=3m,
在△AEB中,$\frac{m}{sin\frac{π}{6}}=\frac{AC}{sin(π-β)}$,①
在△ABE中,$\frac{3m}{sin\frac{π}{6}}$=$\frac{1}{sinβ}$,②
由①②,得AC=$\frac{1}{3}$,
在△ABC中,BE2=AB2=AB2+AE2-2AB$•AE•cos\frac{π}{6}$,
∴$\frac{7}{16}=1+A{E}^{2}-AE•\sqrt{3}$,解得AE=$\frac{\sqrt{3}}{4}$或AE=$\frac{3\sqrt{3}}{4}$,
∵cos∠ACB=$\frac{B{C}^{2}+C{A}^{2}-A{B}^{2}}{2•BC•CA}$=$\frac{\frac{7}{9}+\frac{1}{9}-1}{2×\frac{\sqrt{7}}{3}×\frac{1}{3}}$<0,
∴$∠ACB>\frac{π}{2}$,∴B<$\frac{π}{6}$=∠BAE,
∴BE>AE,∴AE=$\frac{\sqrt{3}}{4}$.
點評 本題考查三角形的角及邊長的求法,涉及到正弦定理、余弦定理等基礎知識,考查推理論證能力、運算求解能力,考查化歸與轉化思想、函數與方程思想,是中檔題.


 名校課堂系列答案
名校課堂系列答案科目:高中數學 來源: 題型:解答題
查看答案和解析>>
科目:高中數學 來源: 題型:選擇題
| A. | (42,56] | B. | (20,30] | C. | (30,42] | D. | (20,42) |
查看答案和解析>>
科目:高中數學 來源: 題型:選擇題
 如圖,ABCD是邊長為$2\sqrt{3}$的正方形,點E,F分別是邊BC,CD的中點,將△ABE,△CEF,△ADF分別沿AE,EF,FA折起,使得B,C,D三點重合于點P,若四面體PAEF的四個頂點在同一個球的球面上,則該球的表面積是( )
如圖,ABCD是邊長為$2\sqrt{3}$的正方形,點E,F分別是邊BC,CD的中點,將△ABE,△CEF,△ADF分別沿AE,EF,FA折起,使得B,C,D三點重合于點P,若四面體PAEF的四個頂點在同一個球的球面上,則該球的表面積是( )| A. | 6π | B. | 12π | C. | 18π | D. | $9\sqrt{2}π$ |
查看答案和解析>>
科目:高中數學 來源: 題型:解答題
| 無促銷活動 | 采用促銷方案1 | 采用促銷方案2 | ||
| 本年度平均銷售額不高于上一年度平均銷售額 | 48 | 11 | 31 | 90 |
| 本年度平均銷售額高于上一年度平均銷售額 | 52 | 69 | 29 | 150 |
| 100 | 80 | 60 |
| 售價x | 33 | 35 | 37 | 39 | 41 | 43 | 45 | 47 |
| 銷量y | 840 | 800 | 740 | 695 | 640 | 580 | 525 | 460 |
| $\hat y=-1200lnx+5000$ | $\hat y=-27x+1700$ | $\hat y=-\frac{1}{3}{x^2}+1200$ | |
| $\sum_{i=1}^8{({y_i}}-{\hat y_i}{)^2}$ | 49428.74 | 11512.43 | 175.26 |
| $\sum_{i=1}^8{({y_i}}-\overline y{)^2}$ | 124650 | ||
查看答案和解析>>
科目:高中數學 來源: 題型:填空題
查看答案和解析>>
科目:高中數學 來源: 題型:選擇題
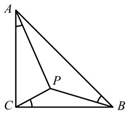 如圖,在等腰直角三角形ABC中,∠C是直角,P是三角形內部一點,且∠CAP=∠BCP=∠ABP=α,則tanα的值等于( )
如圖,在等腰直角三角形ABC中,∠C是直角,P是三角形內部一點,且∠CAP=∠BCP=∠ABP=α,則tanα的值等于( )| A. | $\frac{1}{2}$ | B. | $\frac{\sqrt{2}}{2}$ | C. | $\frac{1}{3}$ | D. | $\frac{\sqrt{3}}{3}$ |
查看答案和解析>>
科目:高中數學 來源: 題型:解答題
查看答案和解析>>
科目:高中數學 來源: 題型:選擇題
| A. | 第一象限 | B. | 第二象限 | C. | 第三象限 | D. | 第四象限 |
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com