
分析 (Ⅰ)由已知得sinBcosA+cosBsinA=sinAsinB⇒sin(A+B)=sinAsinB,即sinC=sinAsinB=$\frac{\sqrt{3}}{2}$,即sinC=$\frac{\sqrt{3}}{2}$,求得:$∠C=\frac{π}{3}$.
(Ⅱ)由$\left\{\begin{array}{l}{{a}^{2}+{b}^{2}-2abcosC=10}\\{a+b=ab}\end{array}\right.$⇒ab=5,即可得s△ABC=$\frac{1}{2}absinC=\frac{1}{2}×5×\frac{\sqrt{3}}{2}=\frac{5\sqrt{3}}{4}$.
解答 解:(Ⅰ)∵$\frac{1}{tanA}$+$\frac{1}{tanB}$=1,∴$\frac{cosA}{sinA}+\frac{cosB}{sinB}=1$.
∴sinBcosA+cosBsinA=sinAsinB⇒sin(A+B)=sinAsinB,
即sinC=sinAsinB,又sinAsinB=$\frac{\sqrt{3}}{2}$,∴sinC=$\frac{\sqrt{3}}{2}$,0$<C<\frac{π}{2}$,
得:$∠C=\frac{π}{3}$.
(Ⅱ)∵c=$\sqrt{10}$,且$\frac{1}{a}$+$\frac{1}{b}$=1,∴$\left\{\begin{array}{l}{{a}^{2}+{b}^{2}-2abcosC=10}\\{a+b=ab}\end{array}\right.$⇒(a+b)2-3ab=10.
∴(ab)2-3ab-10=0,∴ab=5或ab=2(不合)
∴s△ABC=$\frac{1}{2}absinC=\frac{1}{2}×5×\frac{\sqrt{3}}{2}=\frac{5\sqrt{3}}{4}$.
點評 本題考查了三角恒等變形、余弦定理,面積計算,屬于中檔題.


 每日10分鐘口算心算速算天天練系列答案
每日10分鐘口算心算速算天天練系列答案科目:高中數學 來源: 題型:選擇題
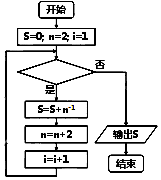
| A. | i>10 | B. | i<10 | C. | i<20 | D. | i>20 |
查看答案和解析>>
科目:高中數學 來源: 題型:解答題
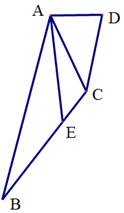 在四邊形ABCD中,點E在BC上,∠BAD=$\frac{2π}{3}$,AD:AC:CD=1:2:$\sqrt{3}$.
在四邊形ABCD中,點E在BC上,∠BAD=$\frac{2π}{3}$,AD:AC:CD=1:2:$\sqrt{3}$.查看答案和解析>>
科目:高中數學 來源: 題型:選擇題
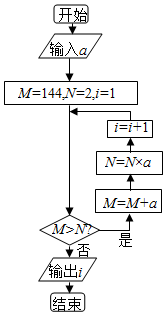 執行如圖所示的程序框圖,若輸出的i=3,則輸入的a(a>0)的取值范圍是( )
執行如圖所示的程序框圖,若輸出的i=3,則輸入的a(a>0)的取值范圍是( )| A. | [9,+∞) | B. | [8,9] | C. | [8,144) | D. | [9,144) |
查看答案和解析>>
科目:高中數學 來源: 題型:解答題
查看答案和解析>>
科目:高中數學 來源: 題型:解答題
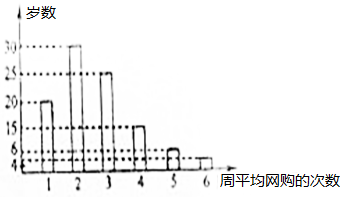 網購是當前民眾購物的新方式,某公司為改進營銷方式,隨機調查了100名市民,統計其周平均網購的次數,并整理得到如下的頻數直方圖.這10名市民中,年齡不超過40歲的有65人.將所抽樣中周平均網購次數不小于4次的市民稱為網購迷,且已知其中有5名市民的年齡超過40歲.
網購是當前民眾購物的新方式,某公司為改進營銷方式,隨機調查了100名市民,統計其周平均網購的次數,并整理得到如下的頻數直方圖.這10名市民中,年齡不超過40歲的有65人.將所抽樣中周平均網購次數不小于4次的市民稱為網購迷,且已知其中有5名市民的年齡超過40歲.| 網購迷 | 非網購迷 | 合計 | |
| 年齡不超過40歲 | |||
| 年齡超過40歲 | |||
| 合計 |
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com