
分析 (1)直線l的參數方程為$\left\{\begin{array}{l}{x=2-\frac{2\sqrt{5}}{5}t}\\{y=1+\frac{\sqrt{5}}{5}t}\end{array}\right.$(t為參數),消去參數t可得普通方程.由曲線C:$\frac{{x}^{2}}{4}$+y2=1,令x=2cosθ,y=sinθ,可得參數方程.
(2)設M(2cosθ,sinθ),可得點M到直線l的距離d=$\frac{4-2\sqrt{2}sin(θ+\frac{π}{4})}{\sqrt{5}}$,利用三角函數的單調性值域即可得出.
解答 解:(1)直線l的參數方程為$\left\{\begin{array}{l}{x=2-\frac{2\sqrt{5}}{5}t}\\{y=1+\frac{\sqrt{5}}{5}t}\end{array}\right.$(t為參數),消去參數t可得普通方程:x+2y-4=0.
由曲線C:$\frac{{x}^{2}}{4}$+y2=1,令x=2cosθ,y=sinθ,可得參數方程:$\left\{\begin{array}{l}{x=2cosθ}\\{y=sinθ}\end{array}\right.$(θ為參數).
(2)設M(2cosθ,sinθ),
∴點M到直線l的距離d=$\frac{|2cosθ+2sinθ-4|}{\sqrt{5}}$=$\frac{4-2\sqrt{2}sin(θ+\frac{π}{4})}{\sqrt{5}}$∈$[\frac{(4-2\sqrt{2})\sqrt{5}}{5},\frac{(4+2\sqrt{2})\sqrt{5}}{5}]$.
點評 本題考查了參數方程的應用、三角函數的單調性值域與和差公式、點到直線的距離公式,考查了推理能力與計算能力,屬于中檔題.


科目:高中數學 來源: 題型:選擇題
| A. | |f(x)-f(a)|≤3|a|+3 | B. | |f(x)-f(a)|≤2|a|+4 | C. | |f(x)-f(a)|≤|a|+5 | D. | |f(x)-f(a)|≤2(|a|+1)2 |
查看答案和解析>>
科目:高中數學 來源: 題型:解答題
查看答案和解析>>
科目:高中數學 來源: 題型:選擇題
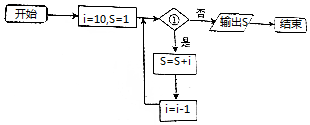
| A. | (5,6] | B. | [5,6) | C. | (6,7] | D. | [6,7) |
查看答案和解析>>
科目:高中數學 來源: 題型:解答題
查看答案和解析>>
科目:高中數學 來源: 題型:填空題
查看答案和解析>>
科目:高中數學 來源: 題型:選擇題
| A. | $\overrightarrow{AB}∥\overrightarrow{BC}$ | B. | $\overrightarrow{AB}∥\overrightarrow{AD}$ | C. | $\overrightarrow{BC}∥\overrightarrow{AC}$ | D. | $\overrightarrow{AC}∥\overrightarrow{AD}$ |
查看答案和解析>>
科目:高中數學 來源: 題型:解答題
| 無促銷活動 | 采用促銷方案1 | 采用促銷方案2 | ||
| 本年度平均銷售額不高于上一年度平均銷售額 | 48 | 11 | 31 | 90 |
| 本年度平均銷售額高于上一年度平均銷售額 | 52 | 69 | 29 | 150 |
| 100 | 80 | 60 |
| 售價x | 33 | 35 | 37 | 39 | 41 | 43 | 45 | 47 |
| 銷量y | 840 | 800 | 740 | 695 | 640 | 580 | 525 | 460 |
| $\hat y=-1200lnx+5000$ | $\hat y=-27x+1700$ | $\hat y=-\frac{1}{3}{x^2}+1200$ | |
| $\sum_{i=1}^8{({y_i}}-{\hat y_i}{)^2}$ | 49428.74 | 11512.43 | 175.26 |
| $\sum_{i=1}^8{({y_i}}-\overline y{)^2}$ | 124650 | ||
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com