Question

18．定義在R上的奇函數f（x）滿足f（2-x）=f（x），當x∈[0，1]時，f（x）=$\sqrt{x}$．又函數g（x）=cos$\frac{πx}{2}$，x∈[-3，3]，則函數F（x）=f（x）-g（x）的所有零點之和等于（　　）

• A． -$\frac{3}{2}$
• B． -$\frac{1}{2}$
• C． $\frac{1}{2}$
• D． $\frac{3}{2}$

Answer 1

分析 利用奇偶性和對稱性作出f（x）和g（x）的函數圖象，利用周期性得出F（x）的零點間的關系，計算F（x）在（0，1）上的零點即可得出零點之和．

解答 解：∵f（2-x）=f（x），
∴f（x）的圖象關于直線x=1對稱，
又f（x）是奇函數，
∴f（x）=f（2-x）=-f（x-2），
∴f（x+4）=-f（x+2）=f（x），
∴f（x）的周期為4．
作出f（x）和g（x）在[-3，3]上的函數圖象如圖所示：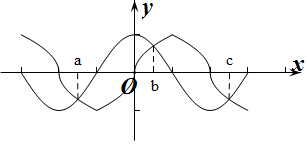

由圖象可知f（x）=g（x）在[-3，3]上有3個零點，
不妨設a，b，c且a＜b＜c，
∵f（x）和g（x）都是周期為4的函數，
∴a=b-2，c=b+2，
∴a+b+c=3b．
∵f（$\frac{1}{2}$）=$\sqrt{\frac{1}{2}}$=$\frac{\sqrt{2}}{2}$，g（$\frac{1}{2}$）=cos$\frac{π}{4}$=$\frac{\sqrt{2}}{2}$，
∴b=$\frac{1}{2}$，
∴a+b+c=3b=$\frac{3}{2}$．
故選D．

點評 本題考查了函數零點與函數圖象的關系，函數周期與對稱性性的應用，屬于中檔題．