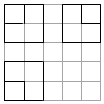
日日人人_亚洲美女在线视频_av手机在线播放_国产大片aaa_欧美中文日韩_午夜理伦三级

精英家教網 > 高中數學 > 題目詳情
9．如圖，正方形網格中，粗實線畫出的是某幾何體的三視圖，若該幾何體的體積為7，則該幾何體的表面積為（　　）
A．18B．21C．24D．27

分析 由三視圖可知：該幾何體為一個棱長為2x的正方體，在一個角去掉一個棱長為x的正方體余下的幾何體．由該幾何體的體積7=（2x）3-x3，解得x．即可得出表面積．

解答 解：由三視圖可知：該幾何體為一個棱長為2x的正方體
在一個角去掉一個棱長為x的正方體，余下的幾何體．
∴該幾何體的體積7=（2x）3-x3，解得x=1．
∴該幾何體的表面積=6×22=24．
故選：C．

點評 本題考查了正方體的三視圖、面積和體積計算公式，考查了推理能力與計算能力，屬于中檔題．

練習冊系列答案
相關習題

科目：高中數學 來源： 題型：選擇題

13．已知P為拋物線y2=4x上一個動點，Q為圓x2+（y-4）2=1上一個動點，當點P到點Q的距離與點P到拋物線的準線距離之和最小時，P點的橫坐標為（　　）
A．$\frac{\sqrt{17}}{8}$B．$\frac{9-\sqrt{17}}{8}$C．$\frac{9}{8}$D．$\sqrt{17}$

查看答案和解析>>

科目：高中數學 來源： 題型：解答題

14．已知定義域為R的函數f（x）=$\frac{{-{2^x}+b}}{{{2^{x+1}}+a}}$是奇函數．
（Ⅰ）求a，b的值；
（Ⅱ）已知f（x）在定義域上為減函數，若對任意的t∈R，不等式f（t2-2t）+f（2t2-k）＜0（k為常數）恒成立．求k的取值范圍．

查看答案和解析>>

科目：高中數學 來源： 題型：解答題

17．數列{an}為正項等比數列，a1=2，$\frac{3}{8}$a4是a2和a3的等差中項，Sn為數列{bn}前n項和，2b2=b1+b3，$\sqrt{{S}_{n}}$是公差為1的等差數列．
（1）求數列{nan}的前n項和Tn；
（2）求數列{bn}通項公式；
（3）是否存在n∈N*，使Sn=an成立？若存在，求出所有n的值，若不存在，說明理由．

查看答案和解析>>

科目：高中數學 來源： 題型：解答題

4．已知函數f（x）=xlnx+ax2-x+a（a∈R）在其定義域內有兩個不同的極值點．
（1）求a的取值范圍．
（2）設f（x）的兩個極值點為x1，x2，證明x1x2＞e2．

查看答案和解析>>

科目：高中數學 來源： 題型：選擇題

14．已知f（x）是定義在R上的減函數，其導函數f'（x）滿足$\frac{f（x）+xf'（x）}{f'（x）}＜1$，則下列結論中正確的是（　　）
A．f（x）＞0恒成立B．f（x）＜0
C．當且僅當x∈（-∞，1），f（x）＜0D．當且僅當x∈（1，+∞），f（x）＞0

查看答案和解析>>

科目：高中數學 來源： 題型：解答題

1．某中學有籃球社，吉他社，傳統文化社，動漫社等多個社團，其中傳統文化社借端午節來臨之際舉行包粽子送祝福活動，隨機調查了高三50名男女生對粽子口味的喜好，統計如下表：
  甜味粽 咸味粽 南國風味
 棗子粽豆沙粽  玫瑰粽 蛋黃粽 豬肉粽 什錦粽
 男生 4 3 1 10 4 3
 女生6  5 5 5 13
（1）按以上統計數據填寫下面的2×2列聯表，并運用獨立性檢驗思想，判斷是否有97.5%把握認為甜味粽和咸味粽的喜好與性別有關系？
  甜味粽咸味粽  合計
 男生   
 女生   
 合計   
參考公式及臨界值表如下：K2=$\frac{n（ad-bc）^{2}}{（a+b）（c+d）（a+c）（b+d）}$，其中n=a+b+c+d
P（K2≥k0）0.150.100.050.0250.0100.0050.001
k02.0722.7063.8415.0246.6357.87910.828
（2）從被調查的50人中對玫瑰粽和什錦粽喜好的同學按照分層抽樣的方法抽取4名同學按順序進行深度調查，則前兩位接受調查的都是喜好玫瑰粽同學的概率是多少？

查看答案和解析>>

科目：高中數學 來源： 題型：選擇題

18．定義在R上的奇函數f（x）滿足f（2-x）=f（x），當x∈[0，1]時，f（x）=$\sqrt{x}$．又函數g（x）=cos$\frac{πx}{2}$，x∈[-3，3]，則函數F（x）=f（x）-g（x）的所有零點之和等于（　　）
A．-$\frac{3}{2}$B．-$\frac{1}{2}$C．$\frac{1}{2}$D．$\frac{3}{2}$

查看答案和解析>>

科目：高中數學 來源： 題型：填空題

19．若直線2ax-by+2=0（a，b∈R）始終平分圓x2+y2+2x-4y+1=0的周長，則ab的最大值是$\frac{1}{4}$．

查看答案和解析>>

同步練習冊答案
主站蜘蛛池模板： 最近韩国日本免费高清观看 | 黄色高清视频在线观看 | 精品二三区 | 免费观看一级毛片 | 精品欧美乱码久久久久久 | 亚洲一区二区三 | 欧美激情精品久久久久久 | 妞干网在线观看 | 中文字幕在线播放第一页 | 三级av | 亚洲成人在线观看视频 | av在线天堂| 午夜免费 | 国产成人一区二区三区 | 网站黄免费 | 久久青青视频 | 亚洲精品三级 | 亚洲免费视频一区二区 | 日韩在线视频观看 | 99精品欧美一区二区三区 | 精品国产乱码久久久久久1区2区 | 精品久久久一区 | 国产在线一 | 毛片在线视频 | 久久久一区二区三区 | 国产伦精品一区二区 | 国产超碰人人爽人人做人人爱 | 国产 日韩 欧美 中文 在线播放 | 亚洲电影在线观看 | 国产一区在线看 | 不卡免费视频 | 天天天天天天天天操 | 亚洲一级电影 | 亚洲日韩视频免费观看 | 91久久久久久久久久久久久久久久 | 色约约精品免费看视频 | av片在线播放 | 日韩在线一区二区三区 | 91久久| 日韩在线视频网站 | 日本免费三片免费观看 |