Question

16．畫出函數y=|x²-2x-3|的圖象，并指出此函數的單調遞增區間．

Answer 1

分析 先把函數y=x²-2x-3化成頂點式，即可直接得出其頂點坐標，分別令x=0，y=0求出圖象與x、y軸的交點，根據其四點可畫出函數的圖象，根據圖象，即可求得函數的單調區間．

解答 解：∵y=x²-2x-3=（x-1）²-4，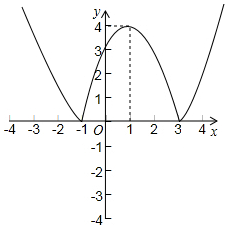
∴y=x²-2x-3圖象開口方向向上，對稱軸x=1，頂點坐標（1，-4），
令x=0得：y=-3，∴與y軸交點坐標（0，-3），
令y=0得：x²-2x-3=0，∴x₁=-1，x₂=3，
∴與x軸交點坐標（-1，0），（3，0），
作出函數y=x²-2x-3的圖象，并把x軸下方的圖象翻折到x軸上方，如圖所示
由圖象可知，函數的單調減區間為（-∞，-1），（1，3）；單調增區間為（-1，1），（3，+∞）．

點評 本題考查的是二次函數的性質，只要根據題意把函數的一般式化為頂點式，在利用翻折變換畫出函數的圖象，便可輕松解答．